R で可視化〜GGally を使った1対1の変数の関係可視化〜
今回は1対1の変数同士の分布の関係の可視化をやってみます。
データは palmerpenguins を使います。このデータは Palmer Archipelago にある3つの島で観測された、3種類のペンギンの身長、体重などのデータです。
可視化
まず、ペンギンデータをロードして欠損を含むサンプルを除いておきます(欠損値値の扱いは主題ではないので)。
library(dplyr); library(tidyverse); library(ggplot2) # スタメンライブラリ
library(palmerpenguins) # データセット
data = penguins %>% na.omit()可視化には GGally パッケージを使います。これは ggplot2 をベースにした可視化パッケージの1つです。まず、どんなものが出るかをみるためにデフォルトのまま実行してみます。
library(GGally)
ggpairs(data)
色々出てきましたが、x 軸の値は対応する列の変数の値、y 軸の値は対応する行の変数の値です。例えば、3行1列目の図は、x 軸がペンギンの種類、y 軸が bill_length_mm(クチバシの長さ)であり、左ブロックのペンギン種は他と比べてクチバシが短いようです(カテゴリの x 軸が頻度になってしまってますが)。ちなみに文字が重なってしまってる目盛のサイズなどは theme() で色々調整できますが、細かいことを調整したらキリがないので放っておきます。
ggpairs の出力結果は、変数の種類の組み合わせによって異なります。上記の図、つまりデフォルトでは以下の通りの図が表示されています。
上三角成分
- カテゴリ×カテゴリ:カテゴリ別の棒グラフ
- カテゴリ×数値:カテゴリ別の箱ひげ図
- 数値×数値:相関係数(信頼区間に基づく検定結果付き)
対角成分
- カテゴリ×カテゴリ:棒グラフ
- 数値×数値:密度
下三角成分
- カテゴリ×カテゴリ:カテゴリ別の棒グラフ
- カテゴリ×数値:カテゴリ別のヒストグラム
- 数値×数値:散布図
図の調整を行う際は、3つのセクションそれぞれに対して、カテゴリ変数と数値の3通りの組み合わせにおける図の種類を指定することで、柔軟な可視化が可能となります。この指定方法は以下のようになります。
ggpairs(data,
# 上三角成分
upper = list(continuous , combo, discrete),
# 対角成分
diag = list(continuous, discrete),
# 下三角成分
lower = list(continuous, combo, discrete))組み合わせによる図の種類は以下項目で設定します。
- カテゴリ×カテゴリ:
discrete - カテゴリ×数値:
combo - 数値×数値:
continuous
本記事では多くのパターンは試しませんが、こちらで詳細をみることができます。それでは以下の設定で ggpairs を実行していきます、太字部分がデフォルトからの変更箇所です。
上三角成分
- カテゴリ×カテゴリ:カテゴリ別の棒グラフ
- カテゴリ×数値:カテゴリ別の箱ひげ図
- 数値×数値:2次元の密度(等高線)
対角成分
- カテゴリ×カテゴリ:棒グラフ
- 数値×数値:ヒストグラム
下三角成分
- カテゴリ×カテゴリ:カテゴリ別の棒グラフ
- カテゴリ×数値:カテゴリ別のヒストグラム
- 数値×数値:信頼区間付き回帰直線と散布図
# 見やすくするため、'year' を除いて図示
ggpairs(data = data[,1:7],
upper = list(continuous = "density", combo = 'box', discrete = 'count'),
diag = list(continuous = 'barDiag', discrete = 'barDiag'),
lower = list(continuous = 'smooth', combo = 'facethist', discrete = 'count'))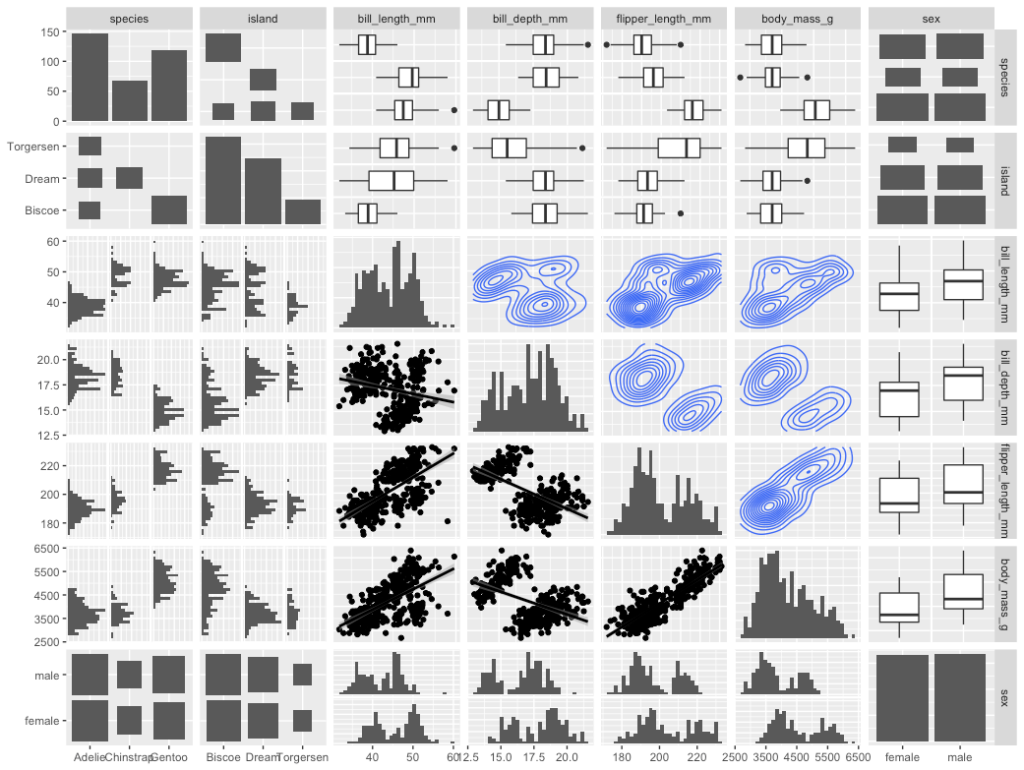
これをベースとしてさらに解釈しやすくするために、種類別に色分けし、透過度をあげたりサイズを調整したりしてみます。各組み合わせの図に対する細かいオプションは、wrap() を使って以下のように組み合わせごとに設定します。
ggpairs(data = data[,1:7], aes(col = species),
upper = list(continuous = wrap("density", alpha = 0.7), combo = 'box', discrete = wrap('count', alpha = 0.7)),
diag = list(continuous = wrap('barDiag', alpha = 0.7), discrete = wrap('barDiag', alpha = 0.7)),
lower = list(continuous = wrap('smooth', size = 0.5, alpha = 0.7), combo = wrap('facethist', alpha = 0.7), discrete = wrap('count', alpha = 0.7)))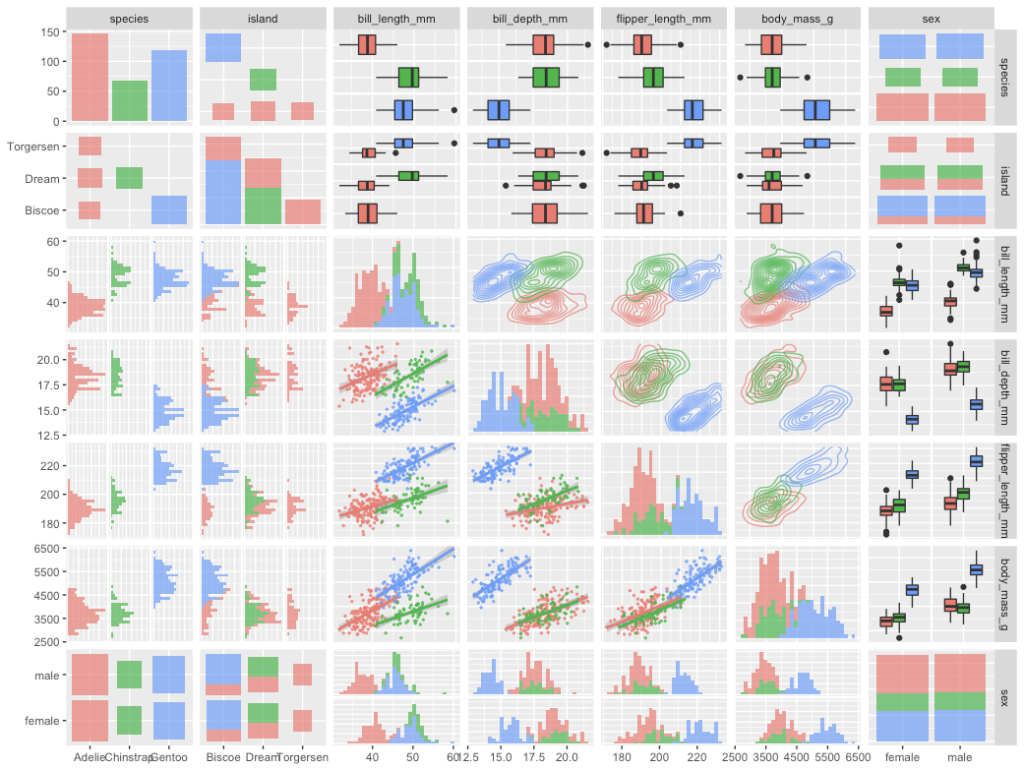
先程の図よりずっと見やすく、また情報が詳細になったのではないでしょうか。特に、bill_length_mm(クチバシの長さ)と bill_depth_mm(クチバシの太さ)などの、全体でみると負の相関になっていますが、種類別に考えると正の相関になるという真逆の結果になっています(シンプソンのパラドックス)。
これらの結果だけでも、単純に species をダミー変数として重回帰分析するだけでは不十分であり、交互作用項の導入、階層化などの対応が必要であることがわかります。
最後に、個人的に一番わかりやすいと思っている図を表示してみます。
ggpairs(data = data[,1:7], aes(col = species),
upper = list(continuous = wrap("cor", size = 3, alpha = 0.7), combo = 'box_no_facet', discrete = wrap('count', alpha = 0.7)),
diag = list(continuous = wrap('densityDiag', alpha = 0.7), discrete = wrap('barDiag', alpha = 0.7)),
lower = list(continuous = wrap('smooth', size = 0.5, alpha = 0.7), combo = wrap('facethist', alpha = 0.7), discrete = wrap('count', alpha = 0.7)))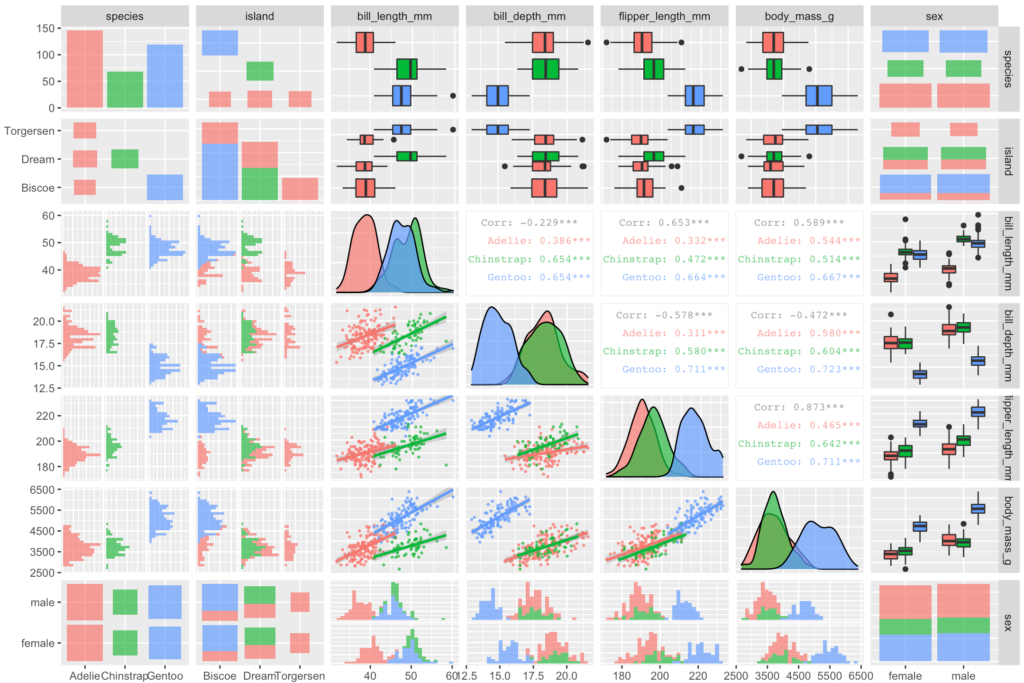
いかがでしょうか、「こんなペアのおすすめもあるよ!」という声がありましたら大歓迎です。