Box-Cox 変換をして、分布や推定されるモデルの特徴を比較
Box-Cox 変換は、正の値を取る変数をより正規分布に近い形に変換するための変数変換方法の一つで、以下の式によって定義されます。
$$z(\lambda) = \begin{cases}
\displaystyle \frac{x^\lambda – 1}{\lambda} & \lambda \neq 0 \\
\log x & \lambda = 0\end{cases}$$
変換が二通りになっていますが、一つ目の式でロピタルの定理を使って \(\lambda \rightarrow 0\) とする極限計算を行うと \(\log x\) となります。
この変換は、あるデータを正規分布に近づけたいときや、モデルを問わず、予測精度を上げるための探索的な前処理の一つとして行われることが多いかと思います。
本記事では、実際に Box-Cox 変換を行い、
1. データの分布
2. 推定されたモデルの特徴
3. 推定された回帰モデルの、テストデータに対する予測精度
の3つを見ていきます。
Bostom の住宅価格データを使って検証
データに関する説明は長くなりそうなので割愛します。要するにボストンの町や部屋の情報と住宅価格の中央値(目的変数)が記録されたデータです。
library(dplyr); library(mlbench)
data(BostonHousing)
(data = as_tibble(BostonHousing))# A tibble: 506 x 14
crim zn indus chas nox rm age dis rad tax ptratio b lstat medv
<dbl> <dbl> <dbl> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.00632 18 2.31 0 0.538 6.58 65.2 4.09 1 296 15.3 397. 4.98 24
2 0.0273 0 7.07 0 0.469 6.42 78.9 4.97 2 242 17.8 397. 9.14 21.6
3 0.0273 0 7.07 0 0.469 7.18 61.1 4.97 2 242 17.8 393. 4.03 34.7
4 0.0324 0 2.18 0 0.458 7.00 45.8 6.06 3 222 18.7 395. 2.94 33.4
5 0.0690 0 2.18 0 0.458 7.15 54.2 6.06 3 222 18.7 397. 5.33 36.2
6 0.0298 0 2.18 0 0.458 6.43 58.7 6.06 3 222 18.7 394. 5.21 28.7
7 0.0883 12.5 7.87 0 0.524 6.01 66.6 5.56 5 311 15.2 396. 12.4 22.9
8 0.145 12.5 7.87 0 0.524 6.17 96.1 5.95 5 311 15.2 397. 19.2 27.1
9 0.211 12.5 7.87 0 0.524 5.63 100 6.08 5 311 15.2 387. 29.9 16.5
10 0.170 12.5 7.87 0 0.524 6.00 85.9 6.59 5 311 15.2 387. 17.1 18.9
# … with 496 more rowsサンプルサイズが506、特徴量が13個あり、目的変数は medv です。
データは以下の通り分割し、全体の20%をテストデータとしました。
set.seed(0)
index_train = sample(c(FALSE, TRUE), size = nrow(data), replace = TRUE, prob = c(0.2, 0.8))
train = data[index_train,]
test = data[!index_train,]1. 分布の比較
car パッケージの powerTransform 関数を使って、正規分布に最も近くなるように変換する λ を推定します。
library(car)
y_train = train$medv
lambda1 = powerTransform(y_train)$lambda0.1742895と推定されました。定義に従って medv を変換します。
# Box-Cox 変換を行う関数
boxcox = function(x, lambda) {
if (lambda == 0) {
x_transformed = log(x)
} else {
x_transformed = (x ^ lambda - 1) / lambda
}
return(x_transformed)
}
z1 = boxcox(x = y_train, lambda = lambda1)理解のために関数を定義しましたが、bcPower() 関数で一発です。
z_bcPower = bcPower(U = y_train, lambda = lambda1)
identical(z1, z_bcPower)
# TRUE(計算結果が同じ)分布がどれほど正規分布に近づいたかを確認するため、1. ヒストグラム、2. 経験分布関数(eCDF)、3. Q-Q Plot を見ていきます。
ここで、標準正規分布を基準に比較するため、Box-Cox 変換したデータを標準化しておきます(これによって主旨が変わることはない)。
y_scale = scale(y_train)
z1_scale = scale(z1)ヒストグラム
まず、適当な横軸の範囲を axis_x として、この範囲で標準正規分布の密度関数を生成します。また、より見た目で比べやすくするために各データの密度もプロットします。density() はカーネル密度推定によってデータから分布を推定してくれる関数です。
axis_x = seq(-3, 3, length.out = length(z1))
dens_normal = dnorm(axis_x, mean = 0, sd = 1)
dens_y = density(y_scale)
dens_z1 = density(z1_scale)
par(mfcol = c(1,2)) # 描写領域を1×2に分割
# 変換前
hist(y_scale, probability = TRUE, breaks = 30, main = '変換前')
lines(dens_y, lwd = 3)
lines(axis_x, dens_normal, col = 2, lwd = 3)
# 変換後
hist(z1_scale, probability = TRUE, breaks = 30, main = '変換後')
lines(dens_z1, lwd = 3)
lines(axis_x, dens_normal, col = 2, lwd = 3)
legend("topleft", legend = c('推定密度', '正規分布'),
col = 1:2, lty = 1, lwd = 3, bg = "transparent")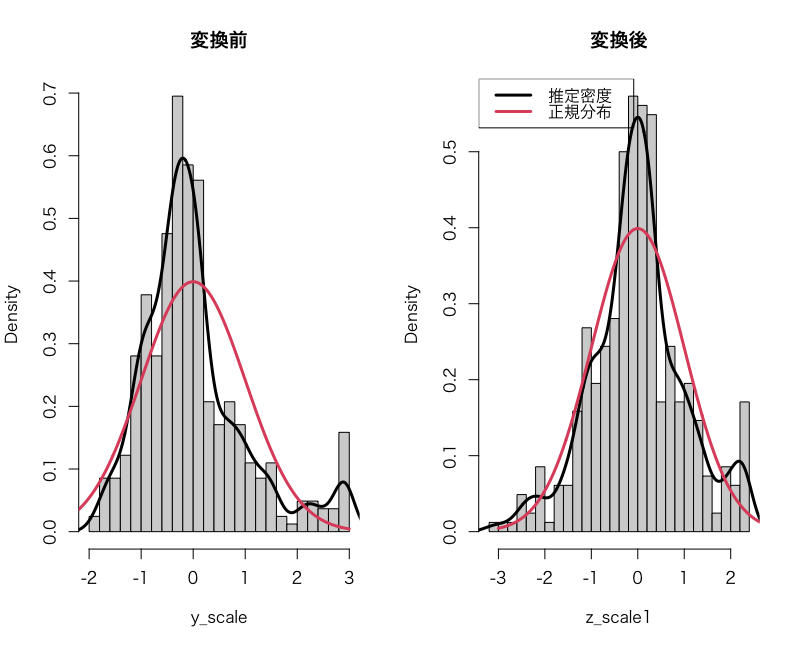
経験分布関数
経験分布関数は、その名の通り「分布関数を経験分布を使って作ったもの」です。手元のデータを使って分布関数を推定するため、カクカクした見た目になります。なお、verticals = TRUE で縦に線を繋いで連続的な分布関数っぽく見せてます。
cdf = pnorm(axis_x)
ecdf_y = ecdf(y_scale)
ecdf_z1 = ecdf(z1_scale)
plot(ecdf_y, do.point = FALSE, verticals = TRUE, main = '変換前')
lines(axis_x, cdf, col = 2)
plot(ecdf_z1, do.point = FALSE, verticals = TRUE, main = '変換後')
lines(axis_x, cdf, col = 2)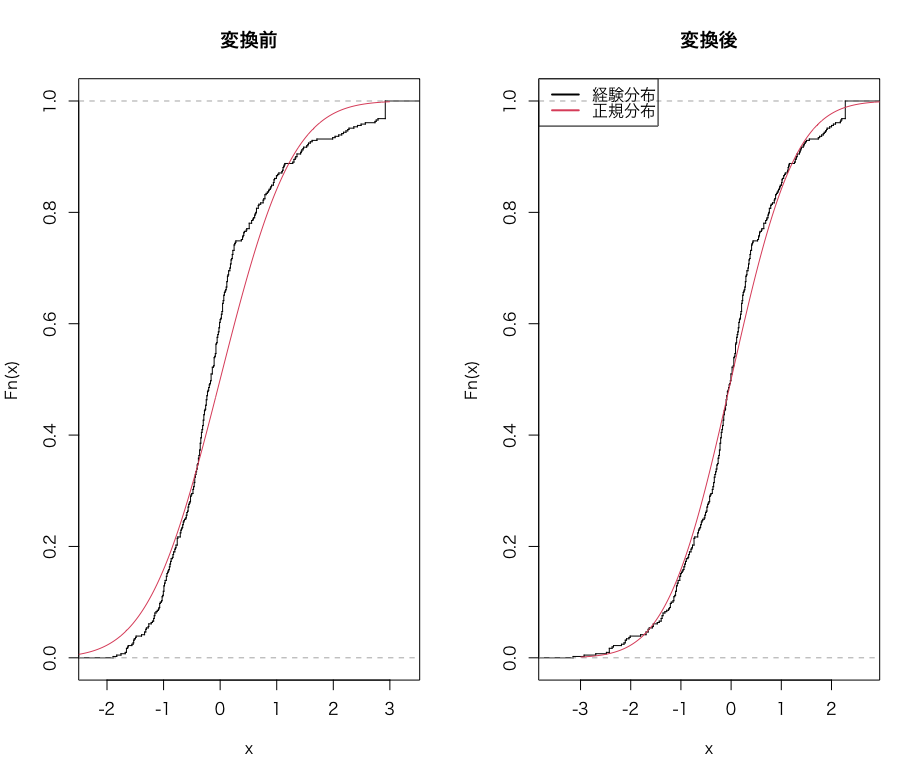
Q-Q Plot
Q-Q Plot は、縦軸を対象データを小さい順に並べたもの、横軸を理論分布の確率点とした散布図です。Q-Q Plot が直線上に並んでいればそのデータは正規分布に従っていると考えられます。
イメージとしては、「データが正規分布に従っていれば、そのデータを小さい順に並べたものと理論分布の確立点は同じ割合の間隔で並んでいるはずだ」といった具合です。
qqnorm(data$medv)
qqline(data$medv)
qqnorm(y_transform1)
qqline(y_transform1)
par(mfcol = c(1,1)) # 描写領域を元に戻しておく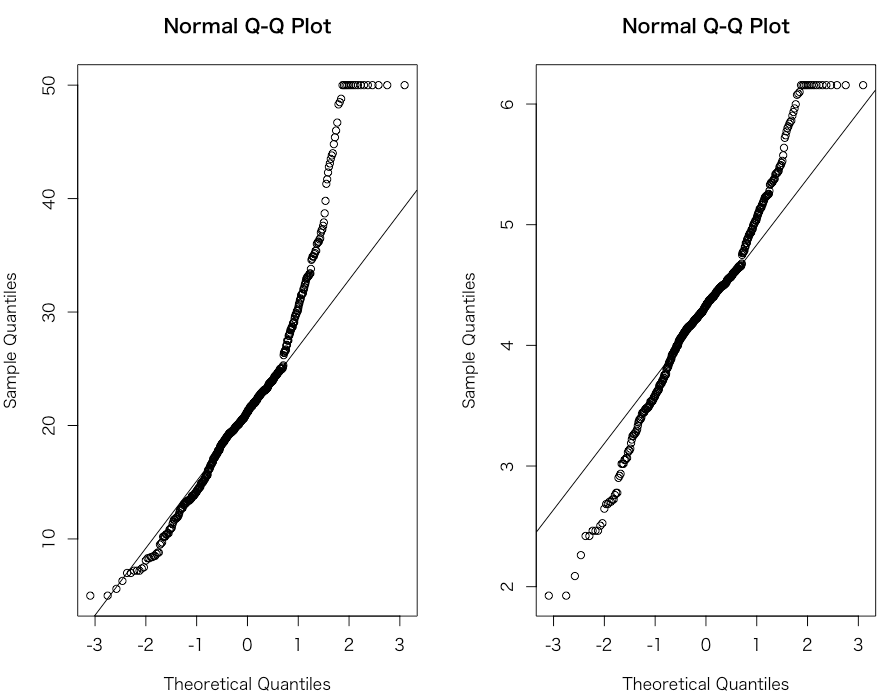
みるときに注意したいのは、この直線は切片0、傾き1の直線に直線上にあれば良いというわけではなく、一般的には直線になっていれば正規分布に従っていると考えます。ちなみに図中の直線はデータの第一四分位数と第三者四分位数を結んだものです。
以上3つの図を見ると、変換後は確かにより正規分布に近づいたように見えます。ただし、最大値が複数あり、そこが右打ち切りのようなデータになってしまっているため、正規分布との乖離の一因となっています。
2. 推定された回帰モデルの比較
回帰モデルを推定し、偏回帰係数やテストデータに対する予測精度を見てみます。
train$z1 = z1
model_y = lm(medv ~ ., data = train[-15])
summary(model_y)
model_z1 = lm(z1 ~ ., data = train[-14])
summary(model_z1)# 実行結果(抜粋)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 39.549376 5.814446 6.802 3.82e-11 ***
crim -0.090720 0.040872 -2.220 0.02701 *
zn 0.050080 0.015307 3.272 0.00116 **
indus 0.032339 0.070343 0.460 0.64596
chas1 2.451235 0.992848 2.469 0.01397 *
nox -18.517205 4.407645 -4.201 3.28e-05 ***
rm 3.480574 0.469970 7.406 7.91e-13 ***
age 0.012625 0.015786 0.800 0.42434
dis -1.470081 0.223349 -6.582 1.48e-10 ***
rad 0.322494 0.077050 4.186 3.51e-05 ***
tax -0.012839 0.004339 -2.959 0.00327 **
ptratio -0.972700 0.148454 -6.552 1.77e-10 ***
b 0.008399 0.003153 2.663 0.00805 **
lstat -0.592906 0.058214 -10.185 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.92 on 396 degrees of freedom
Multiple R-squared: 0.7321, Adjusted R-squared: 0.7233
F-statistic: 83.26 on 13 and 396 DF, p-value: < 2.2e-16Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.8298779 0.3873696 15.050 < 2e-16 ***
crim -0.0128441 0.0027230 -4.717 3.32e-06 ***
zn 0.0025723 0.0010198 2.522 0.012049 *
indus 0.0048897 0.0046864 1.043 0.297407
chas1 0.1724531 0.0661454 2.607 0.009474 **
nox -1.3626406 0.2936458 -4.640 4.73e-06 ***
rm 0.1587795 0.0313103 5.071 6.09e-07 ***
age 0.0009785 0.0010517 0.930 0.352748
dis -0.0868911 0.0148799 -5.839 1.09e-08 ***
rad 0.0231433 0.0051332 4.509 8.61e-06 ***
tax -0.0010074 0.0002891 -3.484 0.000548 ***
ptratio -0.0670723 0.0098903 -6.782 4.34e-11 ***
b 0.0007133 0.0002101 3.395 0.000755 ***
lstat -0.0520780 0.0038783 -13.428 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3278 on 396 degrees of freedom
Multiple R-squared: 0.7826, Adjusted R-squared: 0.7754
F-statistic: 109.6 on 13 and 396 DF, p-value: < 2.2e-165%水準以下で有意になる偏回帰係数はどちらも同じですが、変換後の方が有意確率(P 値)がより小さくなっており、決定係数も高くなっています。
3. 推定された回帰モデルの、テストデータに対する予測精度の比較
次に、未知データに対する予測精度をRMSE, MAE, 決定係数を使ってみてみます。
ここで一つ注意点ですが、Box-Cox 変換を行なったデータで推定した回帰モデルの予測値は、元のスケールに戻す必要があります。
まず準備として、評価指標を返す関数と、Box-Cox 変換の逆を行う関数を定義します。
metrics = function(pred, actual) {
rmse = sqrt((sum(actual - pred) ^ 2) / length(pred))
mae = sum(abs(actual - pred)) / length(pred)
R2 = 1 - sum((actual - pred) ^ 2) / sum((actual - mean(actual)) ^ 2)
result = data.frame(RMSE = rmse, MAE = mae, '決定係数' = R2)
return(result)
}
boxcox_inverse = function(z, lambda) {
y = (lambda * z + 1) ^ (1 / lambda)
return(y)
}テストデータを使った予測と評価を行います。
pred_y = predict(model_y, test)
pred_z1 = boxcox_inverse(z = predict(model_z1, test), lambda = lambda1)
apply(cbind(pred_y, pred_z1), 2, metrics, actual = test$medv)# 実行結果
$pred_y
RMSE MAE 決定係数
1 2.945253 3.08039 0.7740346
$pred_z1
RMSE MAE 決定係数
1 1.260833 2.705093 0.8203987変換データを使ったほうが未知データに対する精度も向上しています。非常にありがたい変換ですね。
ただし、変換したデータで推定した偏回帰係数の解釈には注意が必要です。例えば、x1 の偏回帰係数が1と推定されたからといって、「他の変数を固定した上で、x1が1単位増加すると y の値は平均的に1増える」とはいえなくなり、逆変換した値で考える必要があります。
以上より、Boston の住宅価格データでは、目的変数を Box-Cox 変換により正規分布に近づけた上で線形回帰モデルを推定することで、学習データ、テストデータの両方においてより良くフィッティングできることがわかりました。