【KFAS】タイピングの成長を状態空間モデルで確認
こちらの記事で e-typing でのタイピングスコアの自動取得を行なったので、ほぼ毎日、5回を上限に練習して成績データを溜めてみました。
やはり、データがあれば天下り的に与えられる「スコア」のみではなく、自分なりに様々な視点で自らの成長を確認したいものです。
この記事の執筆時点で60日分のデータ(欠損含む)があり、ほぼ毎日やっているならこの期間でちょっとは成長しているだろうと思われます。
そこで本記事では、簡単な可視化から始め、スコアから誤差や周期的な成分を除去した「本当の実力スコア」を状態空間モデルを使って推定することにより、成長を確認していきます。
使用データと前処理
私のタイピング成績データを使います。
データを読み込み、列名を変更します。
library(dplyr); library(tidyverse)
data_original = read_csv('typing_score.csv', locale = locale(encoding = 'cp932'))
print(data_original, width = Inf, n = 5)
colnames(data_original) = c('date', 'score', 'level', 'time', 'num_correct', 'num_miss', 'wpm', 'accuracy')# A tibble: 237 x 8
date score level time num_correct num_miss wpm accuracy
<chr> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 2021/11/30 416 Professor 51.5 378 7 440. 98.1
2 2021/11/30 445 Professor 50 380 3 456. 99.2
3 2021/11/30 416 Professor 54.9 384 1 420. 99.7
4 2021/11/30 448 Professor 52.5 393 0 449. 100
5 2021/11/30 434 Professor 51.2 383 4 448. 99.0
# … with 232 more rowsデータ収集に関してですが、入力文字の種類、たまたまの実力、気分などの本質的な成長を見る上で邪魔になる要素をなるべく除くため、基本的に1日5回記録を行いました。分析の際は1日の結果を平均したものを代表値として使います。ちなみに「基本的」と言っているのは、たまにサボって3回だけ記録したみたいな日があるからです。
「平均したものを代表値」ですが、具体的には最も細かい粒度のデータである「タイム」「正入力数」「誤入力数」の3つを日毎に平均し、それらから定義通りに「スコア」「WPM」「正確率」を計算します。定義についてはこちらを参照願います。
data_summary = data_original %>%
group_by(date) %>% # 日でグループ化
summarise(time = mean(time),
num_correct = mean(num_correct),
num_miss = mean(num_miss)) %>% # 日毎に平均を計算
mutate(score = 60 * (num_correct - num_miss) / time * ((num_correct - num_miss) / num_correct) ^ 2,
wpm = num_correct * 60 / time,
accuracy = (num_correct - num_miss) / num_correct) # 平均値から各指標を計算また、正月などのだらだら期にはタイピング練習なんてできるはずもないため、そういった日は潔く練習はせず、欠損値として扱います。
data_summary$date = as.Date(data_summary$date)
fulldate = seq(min(data_summary$date), max(data_summary$date), by = 'days') %>%
as.data.frame()
colnames(fulldate) = 'date'
data_withNA = full_join(fulldate, data_summary, by = 'date')
data = data_withNA[,c('date', 'score', 'wpm', 'accuracy')]今回は純粋にスコアで成長を確認するため、可視化の時は WPM、正解率、スコアを使いますが、モデリングの際はスコアのみ使います。
可視化と基本統計量
主題は状態空間モデルなので、ささっと概要確認だけします。
- 現系列プロット
とりあえずどんなデータか見てみます。patchwork は簡単に ggplot を複数描写できる便利パッケージです、ggplot オブジェクトを “+" で繋いで使います。
library(patchwork)
data_gg = gather(data[,1:3], key = variable, value = value, -date)
qplot(date, value, data = data_gg, col = variable, geom = c('line', 'point')) +
qplot(date, accuracy, data = data, geom = c('line', 'point'))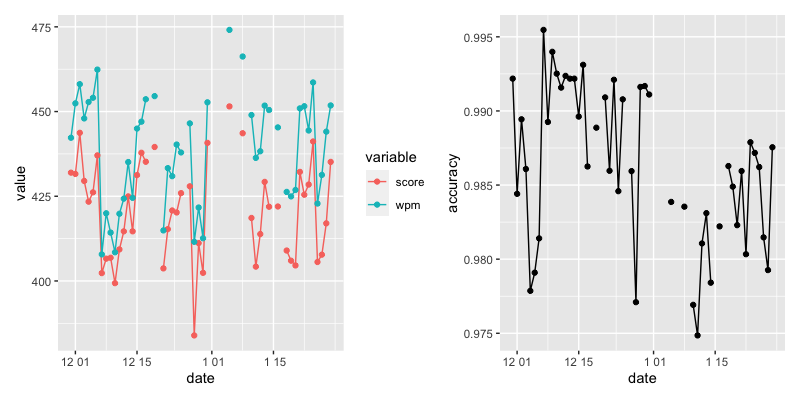
ガタガタしていてよく分かりません、果たして成長しているんでしょうか。
- 後方移動平均
ここで \(n\) 日ごとの統計量を計算するのに便利な rollapply() がある quantmod パッケージを使います。後方移動平均とは、\(n\) 日連続した最後の日の値を \(n\) 日の平均値とする方法です。もちろん、中央、前方もあります。
library(quantmod)
data_ma = data[,c('date', 'score')]
data_ma$n = 1 # 色分けの ID
date_all = data_ma$date
for (n in c(7, 10)) {
ma = rollapply(data$score, width = n, mean, na.rm = TRUE)
data_n = tibble(date = date_all[(length(date_all) - length(ma) + 1):length(date_all)],
score = ma,
n = as.factor(n))
data_ma = rbind(data_ma, data_n)
}
qplot(x = date, y = score, data = data_ma, geom = c('line', 'point'), col = n)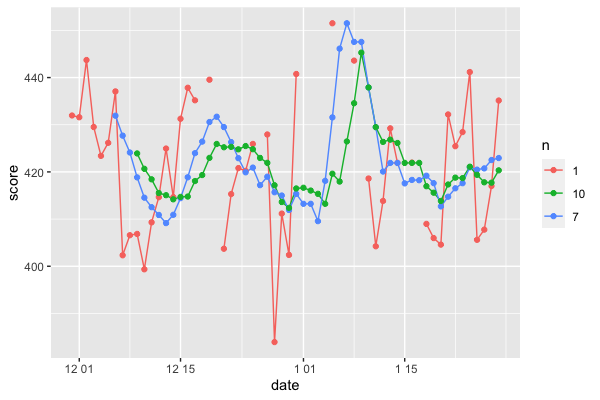
for の中では、\(n\) 日移動平均を計算→元データに縦方向に追記を繰り返しています。移動平均はその定義から \(n\) が大きければ大きいほどなだらかな系列となり、実際にそうなっていることが確認できます。移動平均線を「日毎の誤差が除かれた値=日によらず平均的に出せるスコア」とすると、成長は不安定であり、何か周期的な成分があるように見えます。
- 曜日ごとの平均、週ごとの平均
日付を扱うなら使わない手はない lubridate パッケージを使っています。8行目は Mac で Rstudio を使ってる人だと描画の時に日本語が文字化けしてしまう場合があると思うので、その対策です(Win の人はいらないです)。
library(lubridate)
data_wday = data %>%
mutate(wday = wday(date, label = TRUE)) %>%
group_by(wday) %>%
summarise(score_wday = mean(score, na.rm = TRUE) - 400)
ggplot(data = data_wday, aes(x = wday, y = score_wday)) +
geom_bar(stat = 'identity') +
theme_gray(base_family = "HiraKakuPro-W3")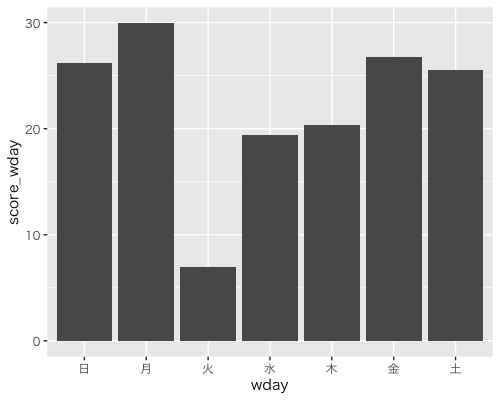
こちらの図では変化がよりわかりやすいように全曜日から400を引いたものをプロットしています(5行目)。火曜にズドンと落ちて、月曜に向かって徐々に上がっているように思えます。実はこれは、 e-typing では毎週火曜日に例文のテーマが変わるため、新たな文章に慣れずにスピードが落ちているためです。
ちなみに、このようにデータの一部を拡大(0~400を切って棒の上の方だけ表示)する方法は、大して変化してないデータをあたかも急上昇しているかのように見せるためのテクニック(ダメなやつ)ですので注意です。
週ごとの平均ですが、今回は火曜〜月曜を1セットとして扱いたいので、week 関数を使わずごり押しで書きます。
week = rep(seq(1,7), ceiling(nrow(data) / 7)) %>% sort()
data_week = cbind(data, week = week[1:nrow(data)]) %>%
group_by(week) %>%
summarise(score_week = mean(score, na.rm = TRUE) - 400)
ggplot(data = data_week, aes(x = week, y = score_week)) +
geom_bar(stat = 'identity')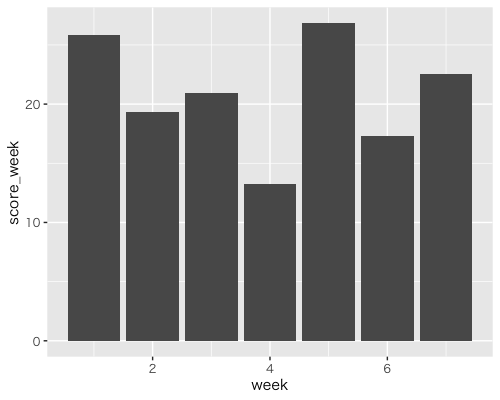
週ごとの平均であれば徐々に右肩上がりになることができますが、随分とガタガタしています。タイピングのテーマに難易度のばらつきがあったり入力者にとっての得意不得意が関係してそうです。
これらの結果から、このデータに関しては
- 可視化だけじゃ成長具合はよくわからない
- 周期的なものがありそう
- 火曜のテーマ変更で下落、その後徐々に伸びてそう(例文への慣れ)
- テーマによってスコアが大きく変わりそう
といったことがわかりました。それでは本題に行きます。
状態空間モデルによる成長確認
状態空間モデルを使って、スコアの系列を分解して解釈していきます。
状態空間モデルは、気温などの直接観測できる観測値と、「本当の水準」といった直接観測はできないけど概念として存在すると考えられる状態変数の2種類の量を扱う時系列モデルです。様々なアイデアを組み込むことができる非常に柔軟なモデルであり、ある系列をいくつかの要因に分解して解釈するといった活用方法があります。本記事でも、観測できない状態変数をいくつか仮定し、状態変数として系列を分解することにより成長を確認していきます。
ちなみに、状態変数は「直接観測できない」と言いましたが、できないというのは環境的、技術的にだったり、要するに分析者が「直接観測できない」と仮定するものです。また、作り方によっては観測値を見かけ上は状態方程式で記述する場合もあります。
今回は数式については触れずにコードを書いていきますが、状態空間モデルについてはとりあえず、「観測値は、1つ以上の潜在変数になんらかの変換を施したものに誤差が乗ったものとして観測される(はず)なので、この関係を利用して逆算的に直接観測できない潜在変数を推定する」というイメージを持っていただけたらと思います。
モデリングのための事前知識と成長の定義
可視化セクションで得た(元からわかってましたが)知見を再掲します。
- 可視化だけじゃ成長具合はよくわからない
- 周期的なものがありそう
- 火曜のテーマ変更で下落、その後徐々に伸びてそう(例文への慣れ)
- テーマによってスコアが大きく変わりそう
これらをモデリングに活かせそうな情報がいくつかありますが、まずは簡単なモデルから試して、徐々に表現力を高めていこうと思います。
また、
スコアから誤差や周期的な成分を除去した「本当の実力のスコア」:= 水準の状態変数の平滑化値
の変化量を成長とします。平滑化値とは、全期間の観測値の情報を使って、一度推定された状態値を修正した値です。
モデル1:ローカル線形トレンドモデル(確率的水準、確定的トレンド)
モデルの気持ち:スコアは、本当の実力スコア(水準)に一定の成長度合い(トレンド)と誤差が加わったものとして観測される
では R の KFAS パッケージを使ってモデルを推定していきます。
model_lt1 = SSModel(data$score ~ SSMtrend(degree = 2, Q = list(matrix(NA), matrix(0))), H = matrix(NA))
fit_lt1 = fitSSM(model_lt1, inits = c(0,0), method = 'BFGS')
res_lt1 = KFS(fit_lt1$model, filtering = c('state', 'mean'),
smoothing = c('state', 'mean'))
# 可視化するデータをまとめる
gg_lt1 = tibble(date = data$date, score = data$score,
level_smooth = res_lt1$alphahat[,'level'],
slope_smooth = res_lt1$alphahat[,'slope'], eps = res_lt1$epshat)H と Q はそれぞれ観測誤差分散、状態誤差分散で、NA にすると最尤推定されます。
結果を保存し、可視化してみます。
lt_fig = ggplot(data = gg_lt1, aes(x = date)) +
geom_point(aes(y = score), lwd = 1.5, alpha = 0.6) +
geom_line(aes(y = level_smooth), col = '4', lwd = 1.5, alpha = 0.6)
lt_fig +
qplot(x = date, y = slope_smooth, data = gg_lt1, geom = 'line') +
qplot(x = date, y = eps, data = gg_lt1, geom = 'line')
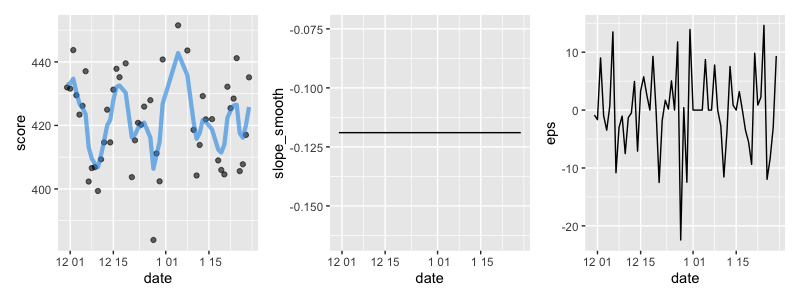
水準成分は滑らかになったとはいえ相変わらずギザギザしており、トレンドに関しては負の値となっているため、この結果だと成長していなそうと考えるのが妥当でしょう。ただ、誤差を見ると定常でも正規分布っぽくもなく、仮定と合っていないためまだまだモデル改善の余地がありそうです。
モデル2:ローカル線形トレンドモデル(確率的水準、確率的トレンド)
モデルの気持ち:スコアは、本当の実力スコア(水準)に局面に応じた成長度合い(トレンド)と誤差が加わったものとして観測される
1を改善して、トレンドを確率的に変動させることで「問題慣れ」の部分を説明することを期待します。
model_lt2 = SSModel(data$score ~ SSMtrend(degree = 2, Q = list(matrix(NA), matrix(NA))), H = matrix(NA))
fit_lt2 = fitSSM(model_lt2, inits = c(0,0,0), method = 'BFGS')
# 他の部分はモデル1と同様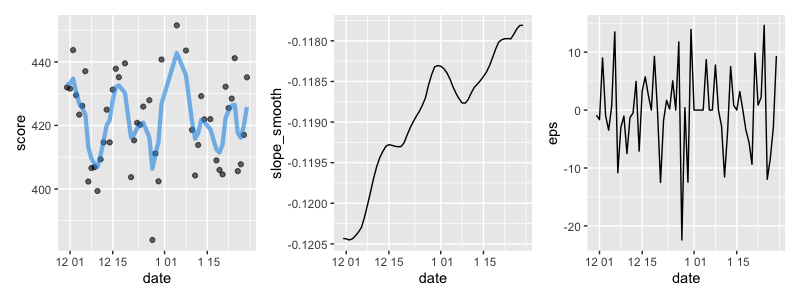
トレンドを確率的にしたところでモデル1とほとんど変わっているように見えません。トレンド成分は変動していますが、値が非常に小さく、影響は微々たるものです。実際、推定された分散を見てみると、
res_lt2$model$Q[2,2,1]
[1] 0.0004441968と非常に小さく、モデル1もモデル2もほとんど変わらないという結果になっています。
モデル3:季節成分モデル
モデルの気持ち:スコアは、本当の実力スコア(水準)にテーマ変更による変動(季節変動)と誤差が加わったものとして観測される
火曜日に文章のテーマ変えが起こり、かつテーマごとに平均的に出せる成績が変わりそうなので、確率的に変動する季節変動を導入します。
# model3
model_seasonal = SSModel(data$score ~
SSMtrend(degree = 2, Q = list(matrix(NA), matrix(0))) +
SSMseasonal(7, sea.type = 'dummy', Q = NA), H = matrix(NA))
fit_seasonal = fitSSM(model_seasonal, inits = c(0,0,0), method = 'BFGS')
res_seasonal = KFS(fit_seasonal$model, filtering = c('state', 'mean'),
smoothing = c('state', 'mean', 'disturbance'))
gg_seasonal = tibble(date = data$date, score = data$score,
level_smooth = res_seasonal$alphahat[,'level'],
season_smooth = res_seasonal$alphahat[,'sea_dummy1'], eps = res_seasonal$epshat)
# 他は同じ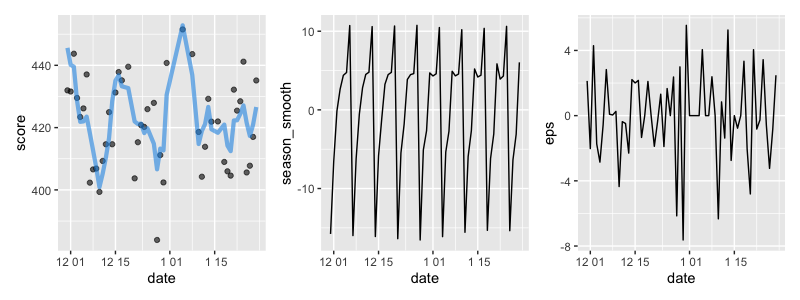
季節成分でちゃんと「火曜に下がって月曜に向かって上がる」を表現できているようです、平準化誤差の絶対値もだいぶ小さくなってきました。ただ、水準成分に関してはギザギザ度合いが強くなってしまっています。水準を確立的にしておくと、どうしてもギザギザしてしまうため、ここを改善する必要がありそうです。
モデル4:基本構造時系列モデル
このモデルは、ローカル線形トレンドモデルの水準成分を確定的としてトレンド成分に確率変動を与え、それに季節成分を加えたものです。水準を確定的、トレンドを確率的とすることで、水準の変動はトレンドによるものとなり、トレンドの変動が緩やかであれば水準の変動も緩やかになるといった特徴があります。経験的にこのモデルによってうまく表現できる系列が多く、このように呼ばれているようです。
model_seasonal2 = SSModel(data$score ~
SSMtrend(degree = 2, Q = list(matrix(0), matrix(NA))) +
SSMseasonal(7, sea.type = 'dummy', Q = NA), H = matrix(NA))
# 他は同じ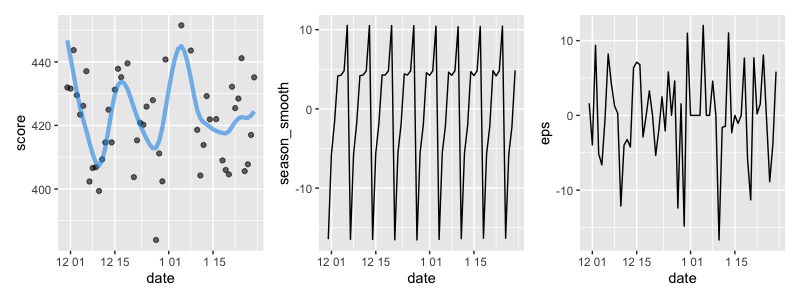
滑らかにはなりました。明らかに周期的なものが残っており、モデルの改善の余地がありそうですが、最初が極端に高く、周期的なものを除けば上昇しているようにも思えます。成長しているんじゃないでしょうか。自分のことは褒めて伸ばしましょう。
参考
KFAS reference manual
KFAS vignette
小野滋. VII. 状態空間モデルの基礎.