2つの正規分布(相関あり or なし)の和、差、積、商の分布を乱数生成で可視化
正規分布に従う2つの独立な確率変数を変数変換した分布は、特性関数を使ったり、同時分布とヤコビアンを使ったりして求められます。しかし、変数間の独立性の仮定をとっぱらっただけで急激に難しくなります。なんなら独立性の仮定があっても積、商の分布の導出はかなり難しいです。もっといえば正規分布じゃなく他の分布なら…と、変数変換後の分布を求める問題は難しくするのが非常に簡単です。
また、たとえば
「標準正規分布に従う確率変数\(X\)の2乗は自由度1のカイ二乗分布に従います(\(X \sim N(0,1) \Rightarrow X^2 \sim \chi^2_1\))」
といわれてもいまいちイメージがつきません。
要するに、数式ベースで変数変換をやってると、難しい(あらゆるところに地雷がある)、分布のイメージがわかりにくい、という難点があります。
なので、本記事では2つの正規分布に着目し、和、差、積、商について、乱数生成によりどんな分布になるか見ることで、なんとなく特徴を理解することにします。
乱数生成と可視化の準備
# 使用モジュール
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import statsデータ生成
mean = [0,0]
cov_non = [[1, 0], [0, 1]]
cov_pos = [[1, 0.8], [0.8, 1]]
cov_neg = [[1, -0.8], [-0.8, 1]]
def wasasekisho_gen(cov, n=5000):
"""二変量正規分布からデータを生成し、変数変換した値を返す関数
"""
x, y = np.random.multivariate_normal(mean, cov, n).T
wa = x + y
sa = x - y
seki = x*y
sho = x/y
return wa, sa, seki, sho, x, yこの関数を使って、正規分布に従う2つの確率変数の和、差、積、商の分布を乱数生成により求めます。また、独立の場合、正の相関を持つ場合、負の相関を持つ場合の3通りで同様の可視化を行います。
独立の場合
$$X \sim N(0, 1), Y \sim N(0,1)$$
以下、理論的に導かれる結論です。
- 和(wa):正規分布
- 差(sa):正規分布
- 積(seki):第二種の変形されたベッセル関数による分布
- 商(sho, x/y):コーシー分布
wa, sa, seki, sho = wasasekisho_gen(cov=cov_non)作成した変数同士の相関とヒストグラムをプロットします。
sns.set(font_scale=2)
sns.pairplot(df)
plt.show()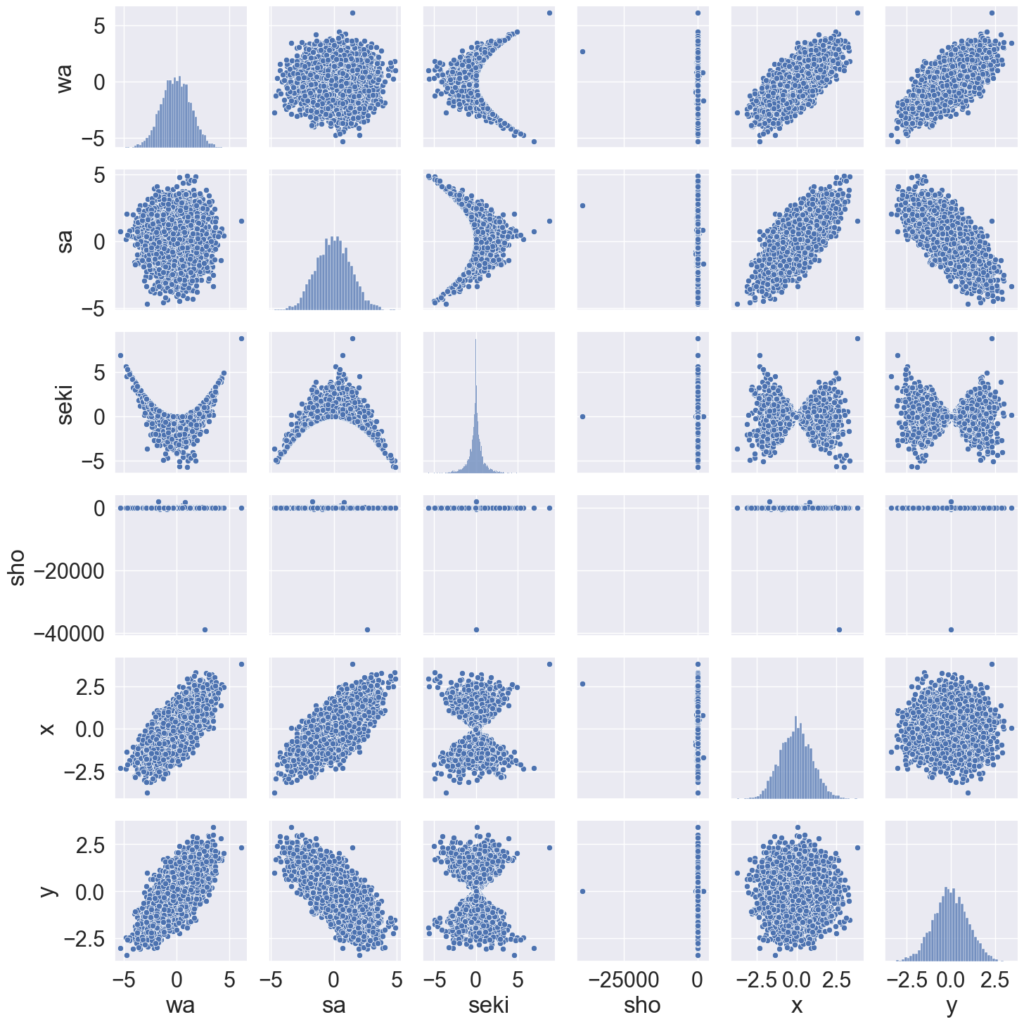
この図は、x軸とy軸それぞれで対応する変数同士の関係を表したものです。たとえば、y軸が"seki"、x軸が"x"のところ(3行5列目)はx-sekiの散布図であり、対角成分はそれぞれの変数のヒストグラムを表します。 なお、下三角部分と上三角部分はx軸とy軸を入れ替えた散布図なので、下三角部分にのみ着目します。
- それぞれの分布について(対角成分)
- 和、差の分布…wa, sa は理論通り見るからに正規分布といった具合で、平均は0、分散は大きくなっています。これは、分散\(\sigma^2\)の正規分布に独立に従う2つの確率変数の差及び和の分散は\(2\sigma^2\)であることと合致します。
- 積の分布…非常に尖度が高そうな分布です。理論分布の「第二種の変形されたベッセル関数による分布」ですが、実は私はこれを初めて知りました。見たところ、平均は真ん中っぽくて、分散も収束しそうな感じです。直感的には、正規分布は0周りに値が密集しているので、その積はさらに0周りに集まりそうです。
- 商の分布…分布が消えたように見えますが、これは大幅な外れ値により、全体的に見ると「0周辺 or 外れ値(複数)」のような分布になっているためです(x軸が0のところに極細の棒が立っています、下図参照)。商だとまれに1 / 0.0001といった場合があるため桁外れに大きな値が生成されています。コーシー分布は期待値、分散が発散してしまう珍しい分布です。
商の分布は棒の数(bins)を100にして拡大するとこんな感じになり、0周辺に値が密集していることがわかります。
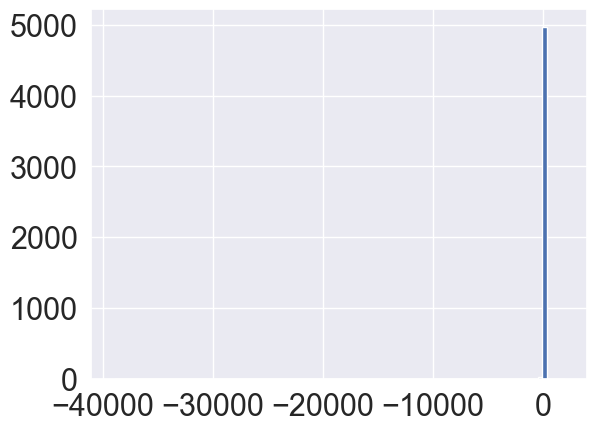
- 変数間の相関について(特徴的なものを選んで箇条書きします)
- 和と差…(私としては)意外なことに、綺麗に球体に分布していて典型的な無相間に見えます。実は、独立な2つの正規分布の和と差の分布はそれぞれ独立に正規分布に従います。このことは変数変換後の同時分布が2つの密度関数の積で分解されることを用いて証明できます。
- 和 or 差と積…二次関数で上限または下限が決められているような関係になっています。こういった関係だと、線形での相関係数の絶対値は非常に小さい値をとりますが、明らかに無相間とは言えません。積の値が大きくなる場合は和の絶対値が大きい場合ですが、和が0周辺をとる場合は「絶対値が近く符号が逆になる場合」→積は大幅にマイナス、「どちらも絶対値が小さい場合」→積は0近くになる、という関係になるので、和が0付近では積は0以下で幅を持って分布することになります。差に関しては符号が逆になるだけで同様の結果です。
- 積とx…積なので、xの絶対値が大きくなると当然分散も大きくなるため、このように徐々に広がっていくような関係になります。
- 商と他…外れ値のせいで全体的に潰れてしまっていますが、積と商に関してはわかりやすい関係があります。商が極端な値をとるのは必ず分母(y)が0に近い値である場合で、積が0に近い値を取るということは少なくともどちらかが0に近い値を取ります。従って、商が外れ値であることは、積が0に近い値を取ることの十分条件と言えそうです。散布図を見ても、商が大きな値を取っているのは積が0付近にある場合のみです。
正の相関を持つ場合
$$\begin{pmatrix} X \\ Y\end{pmatrix} \sim N(\mathbf{0},\begin{pmatrix} 1&0.8 \\ 0.8 & 1\\ \end{pmatrix})$$
コードは共分散行列を変えるだけなので省略します。
以下、理論的に導かれる分布ですが、「不明」というのは私にとってという意味です(どなたか教えていただければ幸いです)。
- 和(wa):正規分布
- 差(sa):正規分布
- 積(seki):不明
- 商(sho, x/y):不明
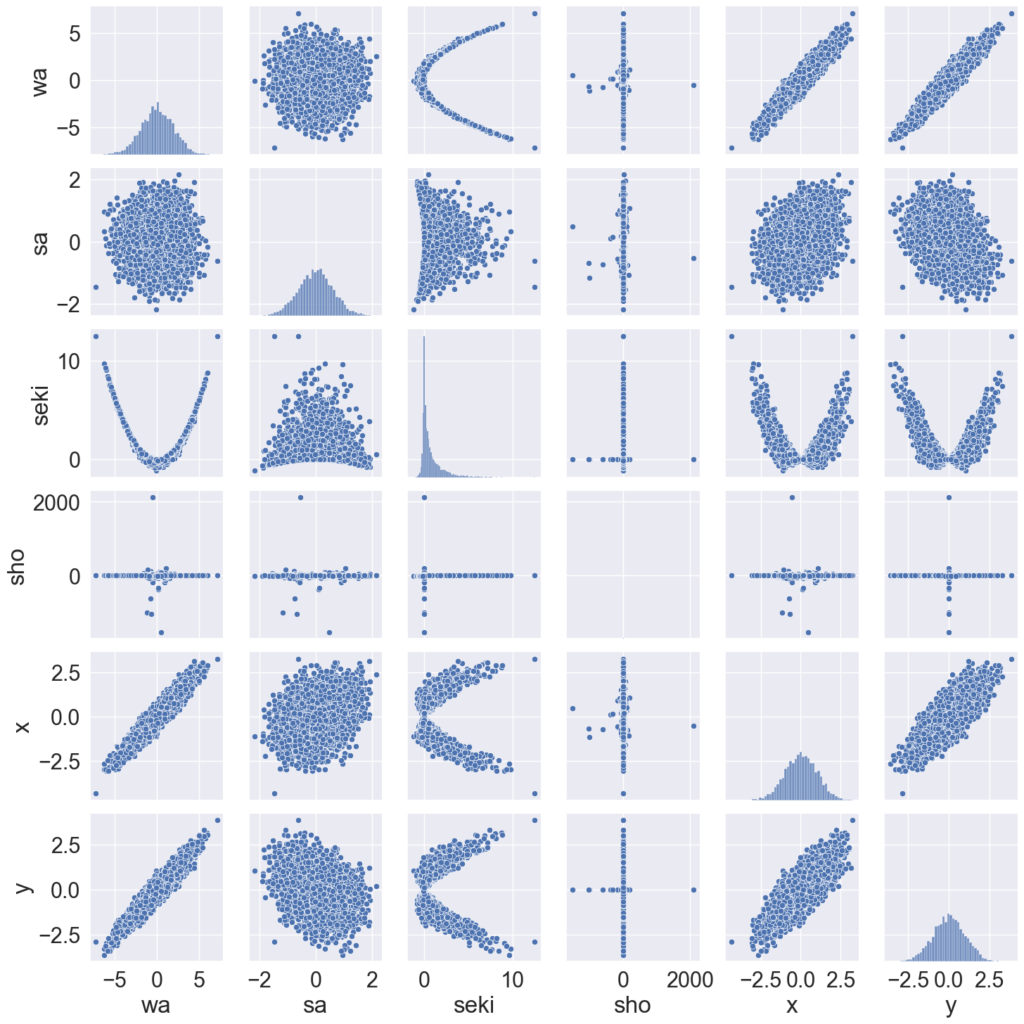
- それぞれの分布について(対角成分)
- 和、差の分布…wa, sa は理論通り正規分布らしいですが、和と差で分散が異なります。和に関しては正の相関を持った変数の和なので、必然的に分散は大きくなります。差に関しては、二つの変数が似るのでその差も小さくなり、結果として分散も小さくなります。
- 積の分布…0付近に密集しているのは無相間の場合と同じですが、値が似るもの同士の積なので大きい方に偏っています(歪度が正)。
- 商の分布…x軸の値を見ると分かる通り、値が似るもの同士の商なので、無相間の場合よりも分散が大幅に小さくなっています。
- 変数間の相関について
- 和と差…無相間の場合と同様、相関があっても正規分布の和と差の分布は無相間に見えます。
- 和 or 差と積…無相間の場合と比べ、和と積に関してはより二次関数によった形となっています。極端な話、完全な相関になればwa = 2x, seki=x^2なのでそれらの関係は2時間数となることがわかります。差に関しては、似たもの同士の差なのでx軸の範囲が狭くなっていること以外は無相間の場合と同様です。
- 積とx…無相間の場合はxが大きくなれば分散も大きくなりましたが、正の相関の場合だとyも一緒に大きくなるので、積の値が正の方向に大きく振れることになります。また、xの絶対値が大きいとyの絶対値も大きい分、分散に関しては無相間の時のような比例関係はなさそうです。
- 商と他…無相間の時と同じ感じです。
負の相関を持つ場合
$$\begin{pmatrix} X \\ Y\end{pmatrix} \sim N(\mathbf{0},\begin{pmatrix} 1&-0.8 \\ -0.8 & 1\\ \end{pmatrix})$$
以下、理論的に導かれる分布です。
- 和(wa):正規分布
- 差(sa):正規分布
- 積(seki):不明
- 商(sho, x/y):不明
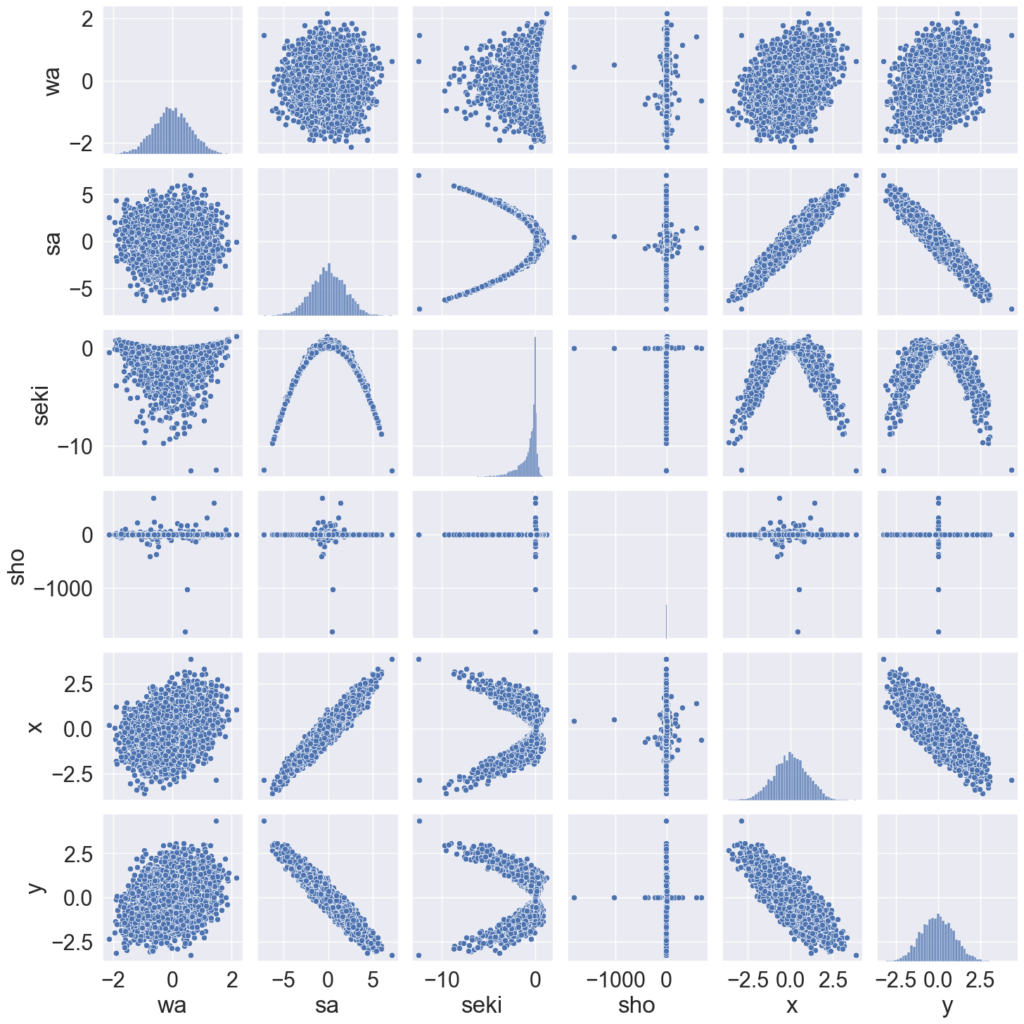
- それぞれの分布について(対角成分)
- 正の相関の場合と逆です。
- 変数間の相関について
- こちらも大体正の相関の場合の逆を言えば当てはまります。
感想
変数変換結果を文章や数式で眺めるよりも分布のイメージがより具体的になりました。また、正の相関、負の相関を持った場合は陽に密度関数をかくのは至難の技ですが、分布を見るとどれも直感的に理解できる特徴を持っていることがわかります。反響があれば他の分布に関しても色々やってみようかと思います。