二項分布の正規近似条件について
はじめに
Kです。
二項分布は、特定の条件下では正規分布で近似できる事が知られています。
二項分布はベルヌーイ分布の和の分布であり、nが大きい時は中心極限定理によって正規分布に近づくためです。
しかし、すべての二項分布が正規分布で近似できるわけではありません。
統計学入門(東京大学出版)のp171によると、実用上の正規近似可能条件は、
「"np > 5″ かつ “n(1-p) > 5" を満たす事」らしいです。
(nはベルヌーイ試行の回数、pはベルヌーイ試行の成功確率)
今回はこちらの条件の妥当性を、Rを使って検証していきます。
検証にあたり、まずは二項分布に従う乱数からヒストグラムを描く関数を定義します。
hist_bin <- function(n, p) {
set.seed(0)
main <- paste("二項分布 (", n, ", ", p, ") のヒストグラム")
binom_sample <- rbinom(n = 100, size = n, prob = p)
hist(binom_sample, main = main)
return(binom_sample)
}rbinom() 関数では、n(ベルヌーイ試行の回数)がsizeという引数になっている点にお気をつけください。
この関数では、二項分布 (n,p) から100回サンプリングを行い、値を返します。
同時に、得られたサンプルのヒストグラムを描く関数になっています。
npが大きい場合の検証
まずは、(n, p) が共に十分に大きい場合の二項分布のヒストグラムを確認してみましょう。
返されたサンプリング結果は、binom_sampleに格納しておきます。
binom_sample1 <- hist_bin(50, 0.5)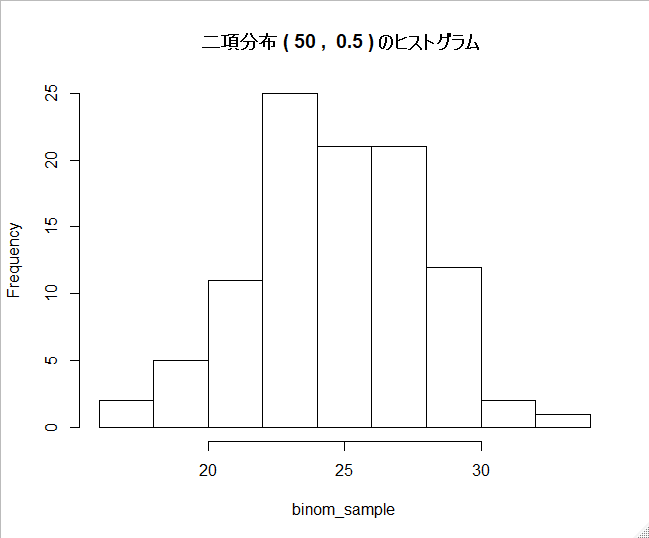
グラフを見た感じだと、正規分布に従っていると言ってしまって良さそうに思えます。
このグラフの場合、np = n(1-p) = 25であり、正規分布近似可能条件も余裕で満たしています。
ここで、本当に正規分布に従っているとしてしまって良いのか、Shapiro-Wilk検定を使って確かめてみます。
詳しくは書きませんが、帰無仮説を「正規分布に従う」とした検定です。
有意水準を5%とした場合、p値が0.05以下の時に帰無仮説が棄却され、元の分布が正規分布に従っていると言えなくなります。
shapiro.test(binom_sample1)# 実行結果
Shapiro-Wilk normality test
data: binom_sample1
W = 0.98543, p-value = 0.3409p値が0.05を超えているので帰無仮説は棄却されず、正規分布とみなしてしまって問題なさそうです。
では、条件を緩めていってみましょう。
近似条件ギリギリで、2つの条件を試してみます。
np = 5 の場合
①n = 10, p = 0.5 の時
binom_sample2 <- hist_bin(10, 0.5)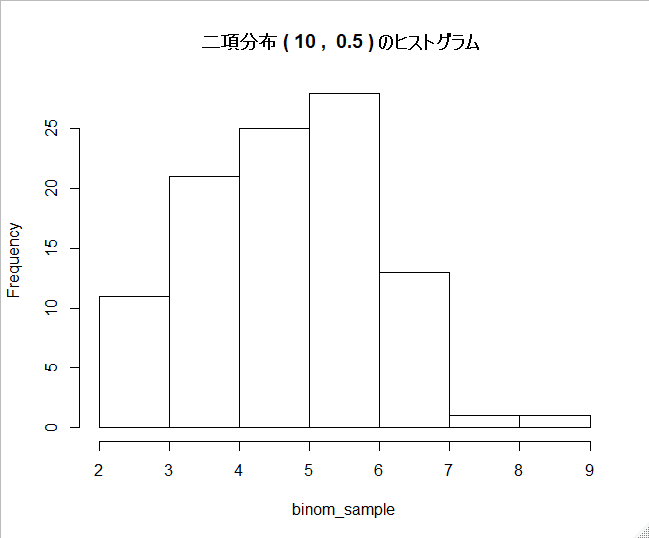
先ほどとは、見た目が大きく変わりました。
正規分布からは、かなり遠ざかったような印象があります。
先ほどと同様に、 Shapiro-Wilk検定を行ってみます。
shapiro.test(binom_sample2)# 実行結果
Shapiro-Wilk normality test
data: binom_sample
W = 0.84901, p-value = 1.09e-08p値が急激に小さくなり、帰無仮説が棄却されるようになりました。
この例だと、正規分布に従っていない、という解釈になります。
②n = 50, p = 0.1 の時
binom_sample3 <- hist_bin(50, 0.1)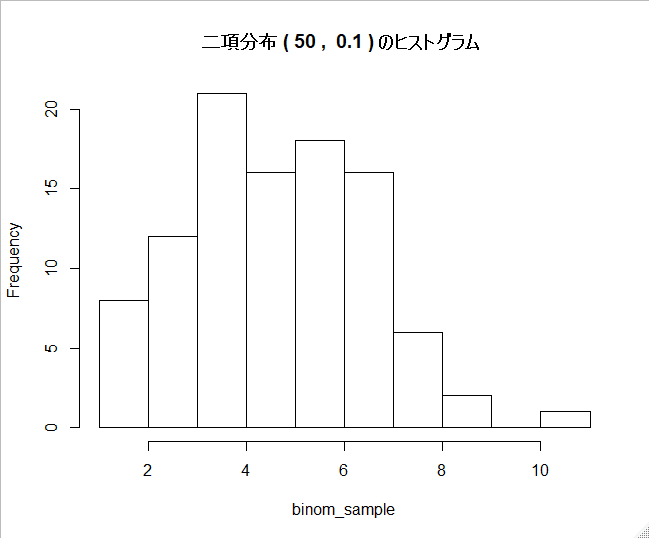
こちらも、正規分布と主張するには無理がありそうな分布になりました。
同様の流れで、 Shapiro-Wilk検定を行います。
shapiro.test(binom_sample3)# 実行結果
Shapiro-Wilk normality test
data: binom_sample3
W = 0.96936, p-value = 0.01974こちらは、帰無仮説が棄却されません。
つまり、正規分布に従っていないとは言えない、という解釈になります。
①と②の例ではどちらも np = 5 の条件を満たしていましたが、異なる結果となりました。
np = 5という条件は、「実用上ギリギリ」のラインなのかもしれません。
元の二項分布と正規近似した分布の、確率の比較
二項分布を正規近似する事で、元の二項分布の上側確率と近似した正規分布の上側確率は、どのように変わるのでしょうか。
はじめの (n = 50, p = 0.5) の例で見た、正規近似できている場合で確認してみましょう。
二項分布 Bin (n = 50, p = 0.5) に従う確率変数 xの上側確率 P(X ≦ x)(xが X以上を取る確率)を求める際に、二項分布から直接計算した確率と、正規近似によって計算した確率を比較してみます。
まずは、それぞれの上側確率を求めて差分を計算する関数を定義しあす。
diff_calculator = function(q_normal, q_binom, n, p) {
prob_normal = 1 - pnorm(q_normal, mean = 0, sd = 1) # 二項分布を正規近似して累積確率を計算
prob_binom = 1 - pbinom(q_binom, size = n, prob = p) # 二項分布のままで累積確率を計算
diff = prob_normal - prob_binom
return(data.frame(diff = diff, diff_rate = diff_rate))
}次に、Bin (n = 50, p = 0.5) の設定で差分を計算し、Xの値ごとの分布をみてみましょう。
n = 50
p = 0.5
# 平均をnp, 分散をnp(1-p)とした正規分布で近似する
q_normal = (1:50 - n * p) / sqrt(n * p * (1 - p))
# 平均をnp, 分散をnp(1-p)とした正規分布で近似する
q_binom = 1:50
result = diff_calculator(q_normal = q_normal, q_binom = q_binom, n = n, p = p)
main = paste("二項分布(", n, ", ", p, ") と、正規分布(", n*p, ", ", n*p*(1-p),") のP値の差のプロット")
plot(result$diff, main=main, xlab="count")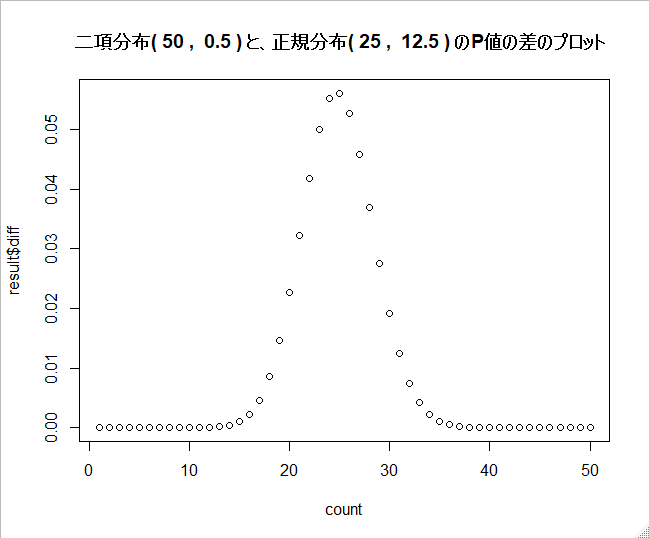
平均値に近い所で、2つの分布の上側確率の乖離が大きくなっています。
乖離が一番大きい平均値付近だと、上側確率が5%程度変わってくる事が分かります。
「コインを50回投げた時に、表が25回以上出る確率」を推定すると、近似によって結果が5%程ずれてしまうという事ですね。
ただ、25回以上出る確率を推定したい事はほぼないと思うので、実用上は問題なさそうに思えます。
最後に
今回の検証では、二項分布において実用上の正規近似可能条件とされている、
「"np > 5″ かつ “n(1-p) > 5" を満たす事」 について検証しました。
検証の結果は、上記の条件を満たしていても正規分布とはみなせない場合がある、という結論です。
1点注意すべき事は、今回使った Shapiro-Wilk検定 は、検定に用いるサンプル数によって結果が変動するという事です。
今回は二項分布からのサンプル数を100として検定を行いましたが、サンプル数を大きくした場合、帰無仮説を棄却しやすく(≒ 正規分布とみなしづらく)なりました。
例えばはじめの np = 25 の条件でも、サンプル数を1,000にした場合、帰無仮説が棄却される事が多くなりました。
Shapiro-Wilk検定 について理解を深めつつ、サンプル数を変化させた時の挙動を見てみるのも面白いかもしれません。
参考文献
・統計学入門
・http://cse.naro.affrc.go.jp/takezawa/r-tips/r/63.html
・http://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2015/dataanalysis/L8.pdf