R と Python で次元削減手法 UMAP を使ってみる
解釈のため、予測制度向上のため、データサイズ削減のためなど、次元削減は特徴量が大量にあることが多い現在ではますます注目されている手法ではないでしょうか。
PCA、LDA、t-SNE など次元削減の方法は色々とありますが、本記事ではタイトルにある通り比較的新しい手法である UMAP で色々と遊んでみます。
ちなみに、私は UMAP の数学的な仕組みについて全く理解していません。
UMAP のアルゴリズムを知るためにまずお手軽に Qiita を参照しましたが、大抵は t-SNE と比べて色々と都合がいいと述べ、アルゴリズムは元論文参照といった流れの記事です。
やれやれと思いながら元論文を呼んでみましたが、なるほど、全然読めません。皆さんのお気持ちがわかりました。
なので、本記事は理論的な説明は一切なしのパッケージで遊ぼな内容です。
注意
本記事では「分類」という言葉をよく使いますが、そもそも今回紹介する手法は目的変数との関係を見て次元圧縮をしているわけではなく、「圧縮後のデータが目的変数ごとに綺麗に分かれている=良い圧縮方法」としているわけではありません。例えば、目的変数とは無関係かつデータごとに顕著に異なる変数を使えば、次元削減した結果はうまくデータのグループが分かれることがありますが、目的変数は各グループに散らばっている可能性があります。
UMAP の特徴
論文では、「実用的な部分を理解したい場合はアルゴリズム部分をスキップしときな」と助言した上で、
- 位相幾何学、圏論を基にした手法
- t-SNE と違って高速かつ同等の精度でデータ構造を捉える
- 次元削減できるけど、解釈性は PCA とかの単純な手法よりは劣る(因子/主成分負荷量のようなものが計算できない)
- サンプルサイズが小さいとノイズに対して構造化してしまう(星の位置から星座を連想しちゃう感じと似てるよねって論文では言ってる)
- 局所的な構造を高精度に表現できる一方、大域的な構造の表現に関しては適してない
といったことが述べられています。ちなみに、ここで述べられている「構造」とは、位相幾何学や圏論でちゃんと定義できるのかもしれませんが、「ある基準でまとめられたデータグループ」というイメージです。
サンプルサイズが大きく(どれくらいかは謎)、解釈性を重視しない(予測や仮説に活かす)、計算速度が気になる、みたいな状況で活躍しそうです。
ちなみに、 PCA 等で次元削減をし、圧縮されたデータに対して UMAP を行うとよりデータがはっきり分かれる(変換後のデータの分布に異なる特徴が現れる)といった報告もあります(こちらの論文)。
データの準備:ペンギンデータ
ペンギンの体格や種類などが記録されたデータを使います。
library(dplyr); library(tidyverse); library(ggplot2) # スタメンライブラリ
library(palmerpenguins) # データセット
penguins# A tibble: 344 x 8
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex year
<fct> <fct> <dbl> <dbl> <int> <int> <fct> <int>
1 Adelie Torgersen 39.1 18.7 181 3750 male 2007
2 Adelie Torgersen 39.5 17.4 186 3800 female 2007
3 Adelie Torgersen 40.3 18 195 3250 female 2007
# … with 341 more rows8つの変数があり、iris 的な使い方を考えると species が目的変数(3クラスのカテゴリ)、それ以外が特徴量です。
次元削減するにあたって、カテゴリカルデータをダミー変数に変換しておきます。
library(makedummies)
penguins$year = as.factor(penguins$year)
penguins_dummy = penguins %>%
na.omit() %>% # 欠損削除
dplyr::select(island, sex, year) %>% # カテゴリカルデータだけ選択
as.data.frame() %>%
makedummies() %>%
as_tibble() %>%
rename(sex_male = sex) # なぜか sex の列名だけそのままだったので、わかりやすいように改名
print(penguins_dummy, n = 3)# A tibble: 333 x 5
island_Dream island_Torgersen sex_male year_2008 year_2009
<int> <int> <int> <int> <int>
1 0 1 1 0 0
2 0 1 0 0 0
3 0 1 0 0 0
# … with 330 more rowsyear は観測年で int 型(整数)でしたが、こちらもカテゴリとして扱うために最初にファクターに変換してます。
ダミー変数化する際は冗長性を避けるために、全カテゴリに対して該当するなら1を立てるのではなく、カテゴリ数-1個だけダミー化して、どちらにも該当しないなら残りのカテゴリに該当、としています。例えば island だと「Dream でも Torgersen でもない = Biscoe」 といった具合です。
元データと結合してダミー変数化前の変数を削除して、前処理完了。
data = cbind(na.omit(penguins), penguins_dummy) %>%
as_tibble() %>%
dplyr::select(-island, -sex, -year)
print(data, n = 3, width = Inf)# A tibble: 333 x 10
species bill_length_mm bill_depth_mm flipper_length_mm body_mass_g island_Dream island_Torgersen sex_male year_2008 year_2009
<fct> <dbl> <dbl> <int> <int> <int> <int> <int> <int> <int>
1 Adelie 39.1 18.7 181 3750 0 1 1 0 0
2 Adelie 39.5 17.4 186 3800 0 1 0 0 0
3 Adelie 40.3 18 195 3250 0 1 0 0 0
# … with 330 more rowsUMAP
R の場合
# UMAP 実行
data_umap = umap(data[,-1], n_components = 2)
# 次元削減後のデータを2つ取り出す
data_gg = tibble(species = data$species,
x1 = data_umap$layout[,1],
x2 = data_umap$layout[,2])
# 可視化(Python のデフォルト出力に似せるため長くなってます)
ggplot(data = data_gg, aes(x = x1, y = x2)) +
geom_point(aes(col = species), alpha = 0.6, size = 2) +
theme_bw() +
theme(
legend.position = "top",
legend.background = element_rect(colour = "gray")
) +
scale_color_manual(values = c("#0000ff", "#ff8c00", "#228b22"))Python の場合
# インスタンス作成
umapper = umap.UMAP(random_state = 3, n_components = 2)
# UMAP 実行
data_umap = umapper.fit_transform(data.drop(columns = "species"))
# 次元削減後のデータの取り出しと可視化
data_umap_x = data_umap[:, 0]
data_umap_y = data_umap[:, 1]
species = data["species"].values
for n in np.unique(species):
plt.scatter(data_umap_x[species == n],
data_umap_y[species == n],
label = n )
plt.grid()
plt.legend()
plt.show()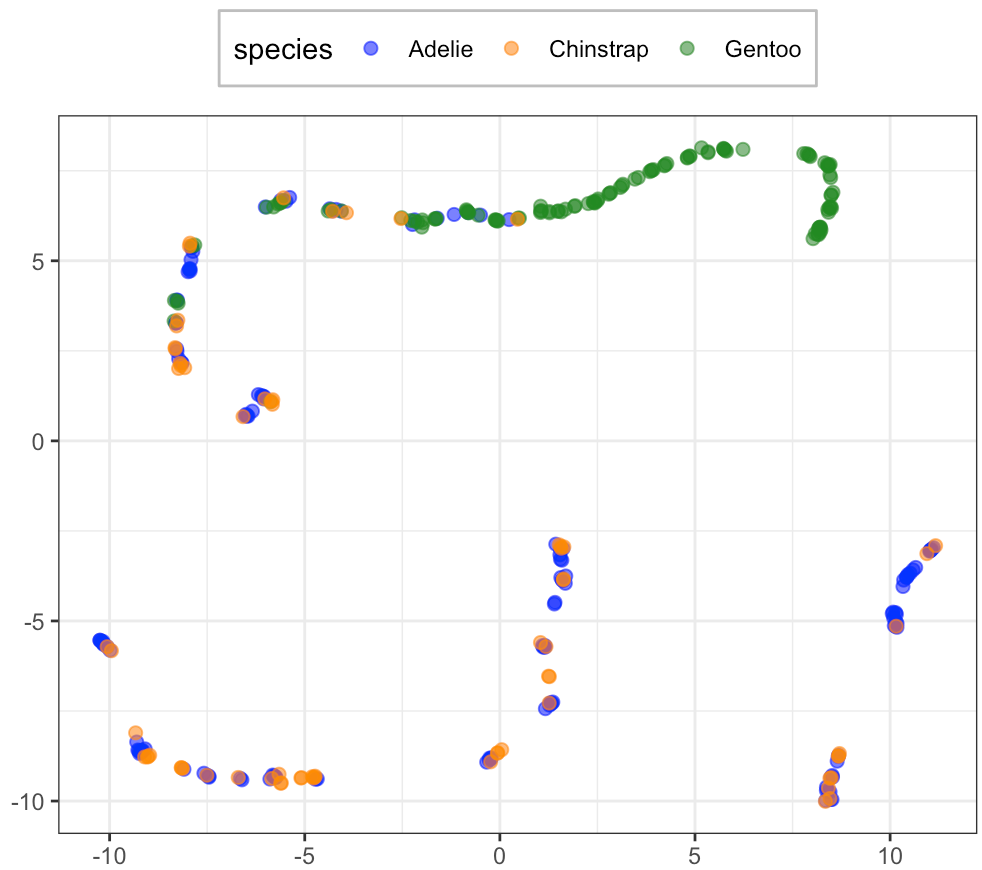
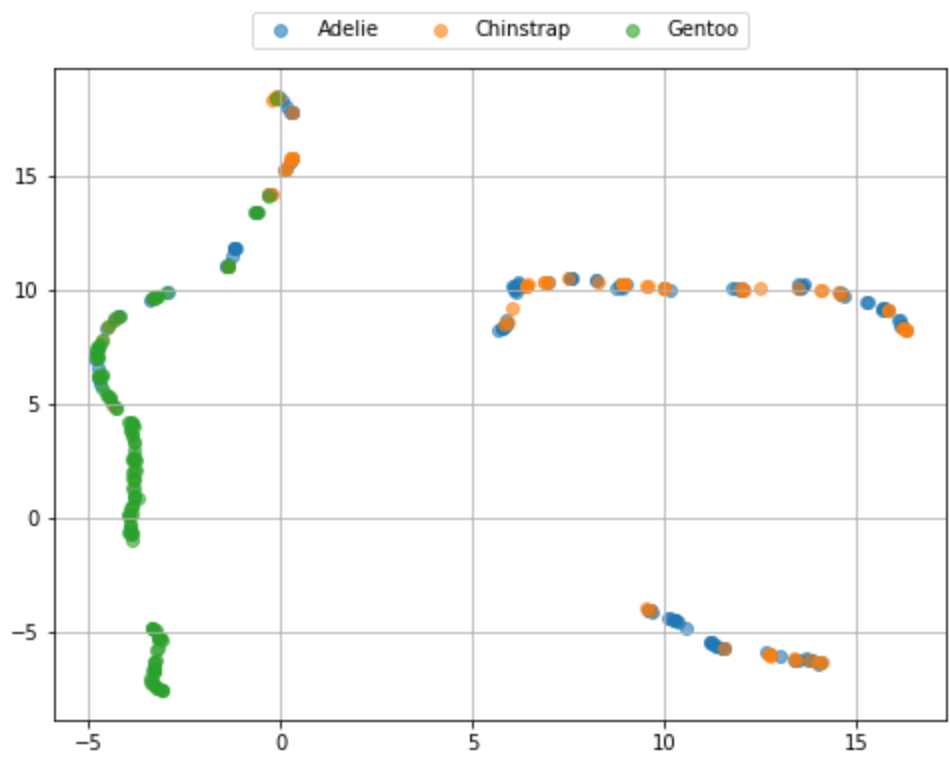
なんらかの構造はありそうに見えますが、種類は混ざってますね。配置が違うのは乱数が違うためです。ちなみに、R で umap(method = "umap-learn") とすれば Python と同様の結果が得られるようです(私の環境だと R が落ちてできませんが)。
PCA だとどう?
ペンギン種類に関してうまく分類できていない理由として、UMAP の特徴として挙げた
- サンプルサイズが小さいとノイズに対して構造化してしまう
- 局所的な構造を高精度に表現できる一方、大域的な構造の表現に関しては適してない
がペンギンデータに当てはまっている可能性が考えられます。
では、線形でシンプルな次元削減手法として有名な PCA(Principal Component Analysis)に登場していただきます。
# PCA 実行
data_pcr = prcomp(x = data[,-1], scale = TRUE)
# PCA の結果から、次元削減後のデータを2つ取り出す
data_gg_pcr = tibble(species = data$species,
pc1 = data_pcr$x[,1],
pc2 = data_pcr$x[,2])
# 可視化
ggplot(data = data_gg_pcr, aes(x = pc1, y = pc2)) +
geom_point(aes(col = species), alpha = 0.6, size = 2) +
theme_bw() +
theme(
legend.position = "top",
legend.background = element_rect(colour = "gray")
) +
scale_color_manual(values = c("#0000ff", "#ff8c00", "#228b22"))
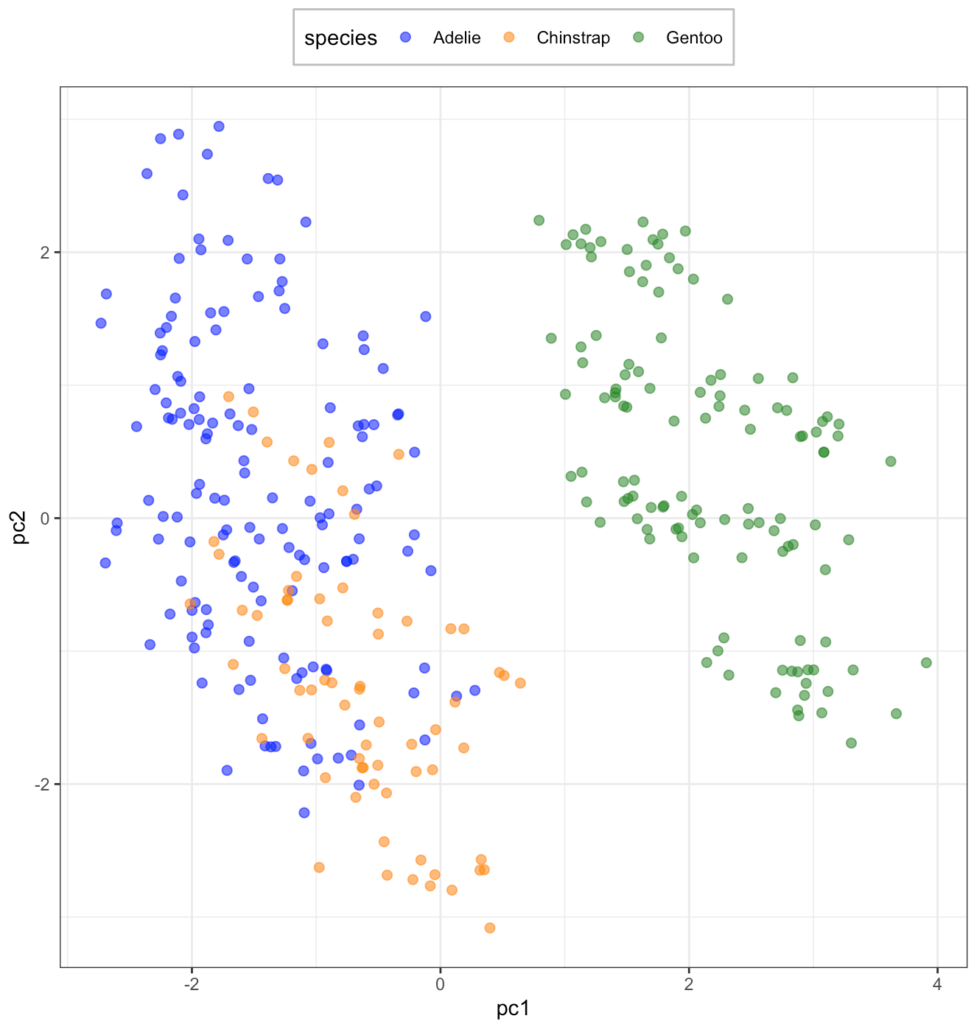
Adellie と Chinstrap は混ざってますが、なかなかよく分類できていそうです。では、複雑に関連してそうな Adelie とChinstrap に絞って UMAP をやってみます。
data_AC = data %>% filter(species %in% c("Adelie", "Chinstrap"))
data_umap = umap(data_AC[,-1], n_components = 2)
data_gg = tibble(species = data_AC$species,
x1 = data_umap$layout[,1],
x2 = data_umap$layout[,2])
ggplot(data = data_gg, aes(x = x1, y = x2)) +
geom_point(aes(col = species), alpha = 0.6, size = 2) +
theme_bw() +
theme(
legend.position = "top",
legend.background = element_rect(colour = "gray")
) +
scale_color_manual(values = c("#0000ff", "#ff8c00", "#228b22"))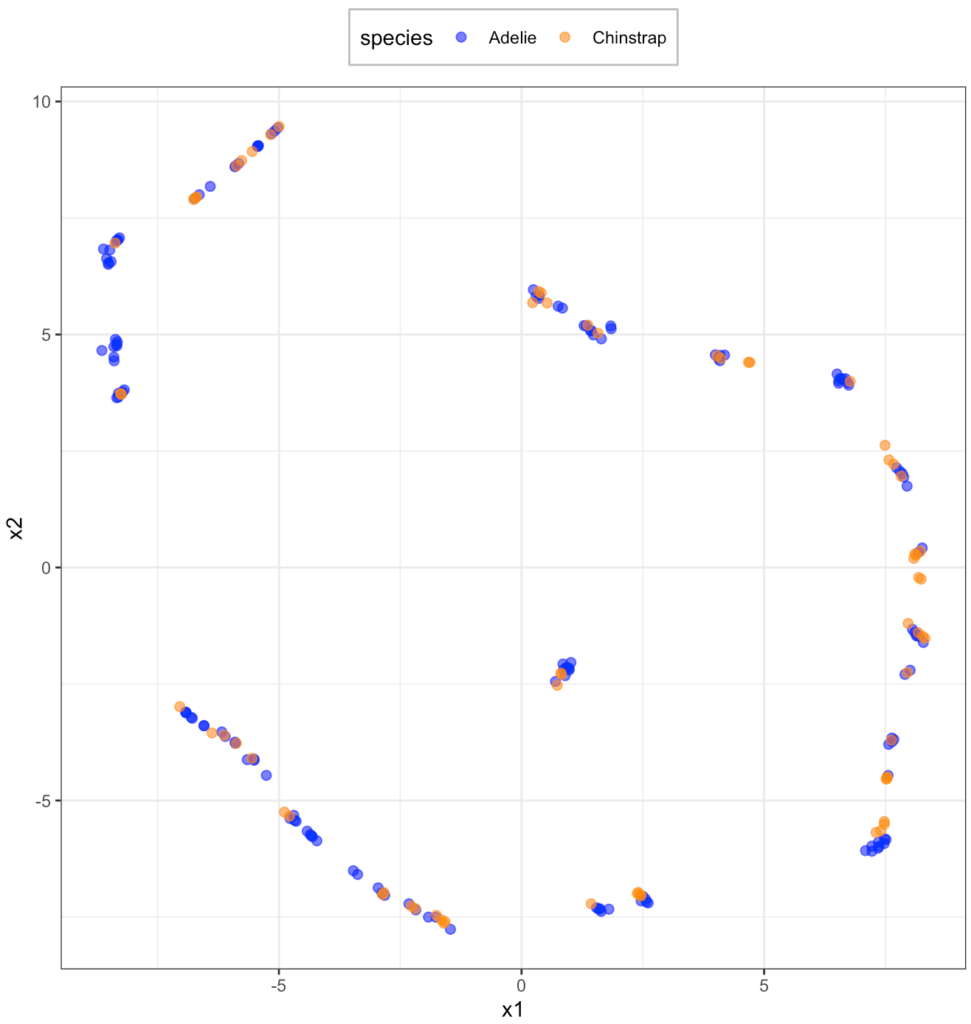
全く分類できてませんね。
特徴量を選んで、UMAP と PCA リベンジ
冒頭の注意で述べた通り、目的変数と関係ない変数があれば、その変数に引っ張られて次元削減後のデータが目的変数に関してうまく別れないといったことがあります。
なので、ペンギンデータに対する EDA の結果をもとに、目的変数と線形では関係なさそうな性別と観測年を除いてやってみた結果が以下の図です。
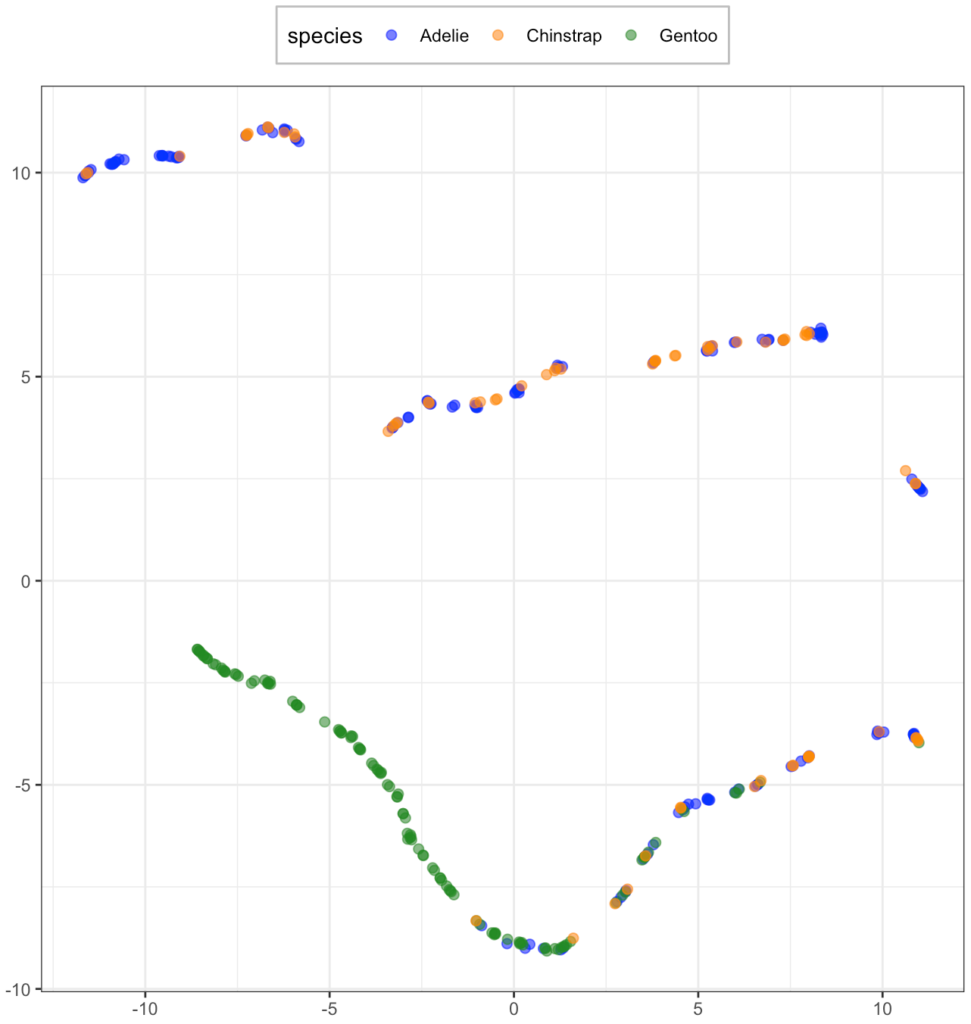
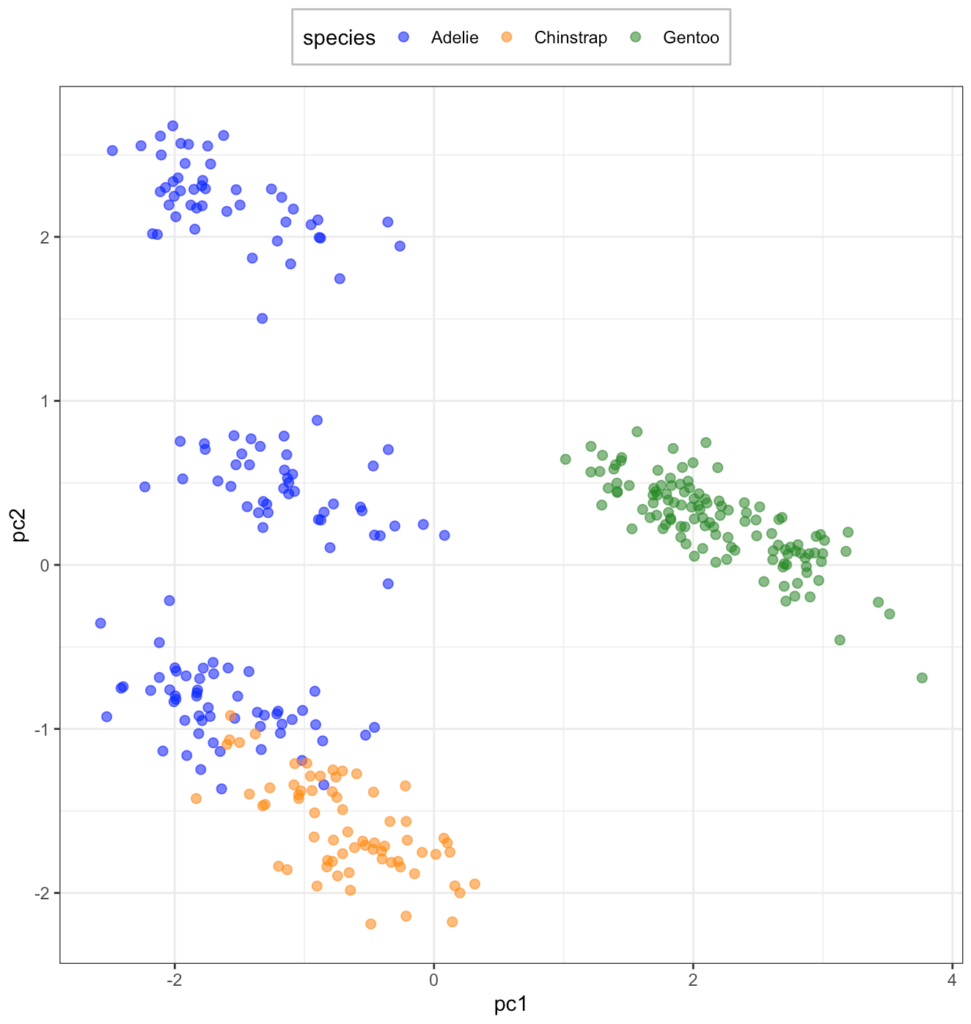
UMAP は相変わらずごちゃごちゃしてますが、PCA はだいぶはっきりと分かれるようになりました。
ただ、PCA でもぱっと見4グループに分かれているように見えることと UMAP の結果を合わせると、ペンギンデータにはあまり目的変数とは関係ないような構造があるかもしれません。
PCA × UMAP
冒頭でチラッと紹介した合わせ技です。
変数を絞って PCA を行い、変換されたデータを寄与度が高い順から2, 4, 6個取り出して UMAP を実行してみます。
これまで載せたコードをちょっといじれば再現できるので、コードは省略します。
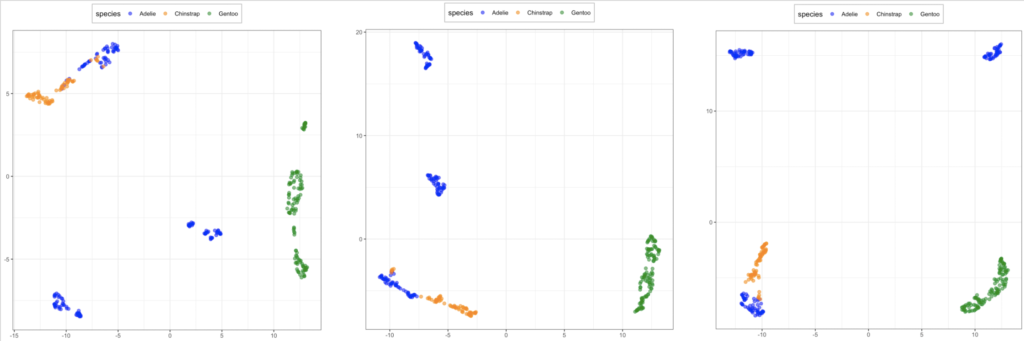
全体として、PCA の結果をさらにぎゅっと縮めた感じになっています。この場合、使う主成分の数を増やせば増やすほど、より遠くに配置されていることがわかります。ただ、PCA との合わせ技は、線形による次元削減をしてから非線形な変換をしているため、元データの非線形構造は無視してしまっているようにも思えます。単純な方法で簡略した後に複雑な手法を適用することの意味がどれほどあるかは考える必要がありそうです。